¿Qué es un análisis de regresión?
Un análisis de regresión genera una ecuación para describir la relación estadística entre uno o más predictores y la variable de respuesta y para predecir nuevas observaciones. La regresión lineal generalmente utiliza el método de estimación de mínimos cuadrados ordinarios, del cual se obtiene la ecuación al minimizar la suma de los residuos al cuadrado.
Por ejemplo, usted trabaja para una compañía de chips de patatas que analiza los factores que afectan el porcentaje de chips desmenuzados por contenedor antes del envío (la variable de respuesta). Usted lleva a cabo el análisis de regresión e incluye el porcentaje de patatas con respecto a otros ingredientes y la temperatura de cocción (grados centígrados) como su dos predictores. La siguiente es una tabla de los resultados.
Análisis de regresión: Chips rotos vs. Pct patatas, Temp cocción
- Por cada aumento de 1 grado centígrado en la temperatura de cocción, se espera que el porcentaje de chips rotos aumente en 0.022%.
- Para predecir el porcentaje de chips rotos para valores de 0.5 (50%) de patatas y una temperatura de cocción de 175 °C, usted calcula un valor esperado de 7.7% de chips de patatas rotos: 4.251 - 0.909 * 0.5 + 0.2231 * 175 = 7.70075.
- El signo de cada coeficiente indica la dirección de la relación.
- Los coeficientes representan el cambio medio en la respuesta para una unidad de cambio en el predictor mientras se mantienen constantes otros predictores incluidos en el modelo.
- El valor p de cada coeficiente prueba la hipótesis nula de que el coeficiente es igual a cero (sin efecto). Por lo tanto, los valores p bajos indican que el predictor es una adición significativa al modelo.
- La ecuación predice nuevas observaciones dados los valores predictores especificados.
Nota
Los modelos con un predictor se denominan regresión simple. Los modelos con más de un predictor se conocen como regresión lineal múltiple.
¿Qué es regresión lineal simple?
La regresión lineal simple examina la relación lineal entre dos variables continuas: una respuesta (Y) y un predictor (X). Cuando las dos variables están relacionadas, es posible predecir un valor de respuesta a partir de un valor predictor con una exactitud mayor que la asociada únicamente a las probabilidades.
- Examinar cómo cambia la variable de respuesta a medida que cambia la variable predictora.
- Predecir el valor de una variable de respuesta (Y) para cualquier variable predictora (X).
¿Qué es regresión lineal múltiple?
La regresión lineal múltiple examina las relaciones lineales entre una respuesta continua y dos o más predictores.
Si el número de predictores es grande, antes de ajustar un modelo de regresión con todos los predictores, se deberían utilizar las técnicas de selección de modelo paso a paso o de los mejores subconjuntos para excluir los predictores que no estén asociados con las respuestas.
¿Qué es la regresión de mínimos cuadrados ordinarios?
En la regresión de mínimos cuadrados ordinarios (OLS), la ecuación estimada se calcula determinando la ecuación que minimiza la suma de las distancias al cuadrado entre los puntos de los datos de la muestra y los valores pronosticados por la ecuación.
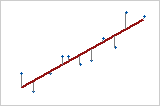
Respuesta vs. Predictor
Con un predictor (regresión lineal simple), la suma de las distancias al cuadrado desde cada punto hasta la línea deben ser tan pequeñas como sea posible.
Supuestos deben cumplirse para regresión OLS
- El modelo de regresión es lineal en los coeficientes. Los mínimos cuadrados pueden modelar la curvatura al transformar las variables (en lugar de los coeficientes). Se debe especificar la forma funcional correcta para poder modelar cualquier curvatura.
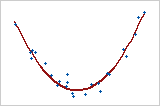
Modelo cuadrático
En este caso, la variable predictora, X, se eleva al cuadrado para modelar la curvatura. Y = bo + b1X + b2X2
- Los residuos tienen una media de cero. La inclusión de una constante en el modelo hará que la media sea igual a cero.
- Todos los predictores no están correlacionados con los residuos.
- Los residuos no están correlacionados entre sí (correlación en serie).
- Los residuos tienen una varianza constante.
- Ninguna variable predictora está correlaciona perfectamente (r=1) con una variable predictora diferente. También es mejor evitar las correlaciones imperfectamente altas (multicolinealidad).
- Los residuos están distribuidos normalmente.
Puesto que la regresión OLS proporcionará las mejores estimaciones solo cuando se cumplan todos estos supuestos, es muy importante evaluarlos. Los métodos comunes incluyen examinar gráficas de residuos, usar pruebas de falta de ajuste y ver la correlación entre los predictores usando el factor de inflación de la varianza (FIV).
