Métodos y fórmulas para la vida útil con respecto al método de porcentaje especificado para el Estudio de estabilidad para lotes fijos

El modelo con tiempo, lote y la interacción tiempo*lote

Cuando el efecto de lote y la interacción lote*tiempo están incluidos en el modelo, el ajuste para el i^ésimo lote en el tiempo x_ij utiliza el siguiente modelo:

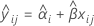
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación inferior y resuelva el tiempo (x).

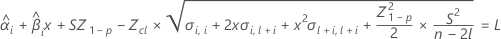
donde

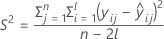
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es estadísticamente mayor que el límite de especificación inferior en tiempo = 0.

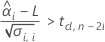
En segundo lugar, Minitab determina si la respuesta media disminuye a una tasa estadísticamente significativa con el tiempo.

En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

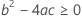
donde

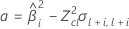
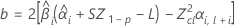
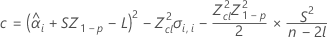
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

El modelo con tiempo y lote

Cuando la interacción lote*tiempo no está incluida en el modelo, las pendientes son iguales para todos los lotes. El ajuste para el i^ésimo lote en el tiempo x_ij utiliza el siguiente modelo:

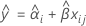
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación inferior y resuelva el tiempo (x).

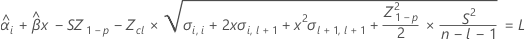
donde

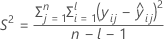
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es estadísticamente mayor que el límite de especificación inferior en tiempo = 0.

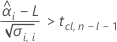
En segundo lugar, Minitab determina si la respuesta media disminuye a una tasa estadísticamente significativa con el tiempo.

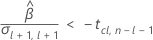
En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

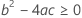
donde

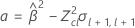
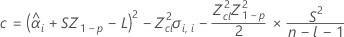
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

El modelo con tiempo

Cuando solo se incluye el tiempo en el modelo, las pendientes y las intersecciones son iguales para todos los lotes. El ajuste en el tiempo x_ij utiliza el siguiente modelo:

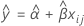
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación inferior y resuelva el tiempo (x).

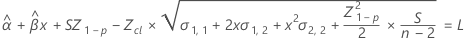
donde

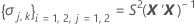
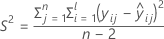
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es mayor que el límite de especificación inferior en tiempo = 0.

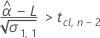
En segundo lugar, Minitab determina si la respuesta media disminuye con el tiempo.

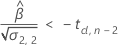
En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

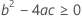
donde

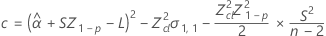
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

Notación

Término	Description
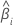	la pendiente para el iésimo lote
Z	el valor de la función de probabilidad acumulada inversa de la distribución normal estándar con la probabilidad dada
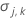	la varianza del vector de parámetros estimados
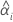	la intersección del iésimo lote
S2	el cuadrado medio del error
L	el límite de especificación inferior
X	la matriz de diseño
i	un índice para mostrar el lote al que corresponde la estimación de vida útil
l	el número de niveles en el factor de lote
n	el número total de valores de respuesta

Para simplificar el cálculo de la vida útil, considere el modelo que se ajusta a los datos.

El modelo con tiempo, lote y la interacción tiempo*lote

Cuando el efecto de lote y la interacción lote*tiempo están incluidos en el modelo, el ajuste para el i^ésimo lote en el tiempo x_ij utiliza el siguiente modelo:

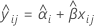
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación superior y resuelva el tiempo (x).

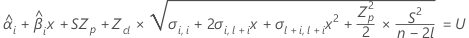
donde

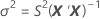
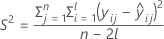
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es estadísticamente menor que el límite de especificación superior en tiempo = 0.

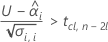
En segundo lugar, Minitab determina si la respuesta media aumenta a una tasa estadísticamente significativa con el tiempo.

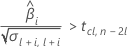
En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

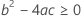
donde

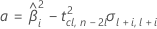
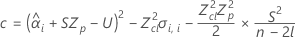
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

El modelo con tiempo y lote

Cuando la interacción lote*tiempo no está incluida en el modelo, las pendientes son iguales para todos los lotes. El ajuste para el i^ésimo lote en el tiempo x^ij utiliza el siguiente modelo:

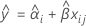
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación superior y resuelva el tiempo (x).

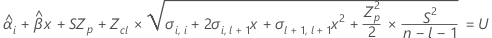
donde

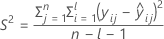
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es estadísticamente menor que el límite de especificación superior en tiempo = 0.

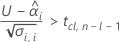
En segundo lugar, Minitab determina si la respuesta media aumenta a una tasa estadísticamente significativa con el tiempo.

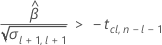
En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

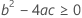
donde

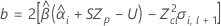
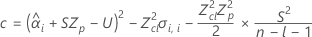
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

El modelo con tiempo

Cuando solo se incluye el tiempo en el modelo, las pendientes y las intersecciones son iguales para todos los lotes. El ajuste en el tiempo x_ij utiliza el siguiente modelo:

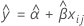
Para hallar la vida útil, establezca la siguiente ecuación igual al límite de especificación superior y resuelva el tiempo (x).

donde

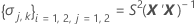
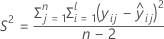
I = el número total de niveles de lote

n = el número total de valores de respuesta

X = la matriz de diseño para el modelo

Para calcular una vida útil significativa, Minitab evalúa tres condiciones. En primer lugar, Minitab determina si la respuesta media es menor que el límite de especificación superior en tiempo = 0.

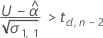
En segundo lugar, Minitab determina si la respuesta media aumenta con el tiempo.

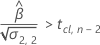
En tercer lugar, Minitab determina si la porción de raíz cuadrada de la ecuación cuadrática tiene una solución en números reales.

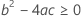
donde

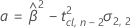
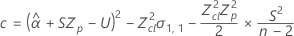
Si se cumplen las tres condiciones, Minitab calcula la vida útil. Para calcular la vida útil, utilice la ecuación cuadrática.

Notación

Término	Description
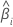	la pendiente para el iésimo lote
Z	el valor de la función de probabilidad acumulada inversa de la distribución normal estándar con la probabilidad dada
	la varianza del vector de parámetros estimados
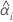	la intersección del iésimo lote
S2	el cuadrado medio del error
U	el límite de especificación superior
X	la matriz de diseño
i	un índice para mostrar el lote al que corresponde la estimación de vida útil
l	el número de niveles en el factor de lote
n	el número total de valores de respuesta

Para simplificar el cálculo de la condición de cómo y cuándo Minitab calcula la vida útil, considere el modelo que se ajusta a los datos.

El modelo con tiempo, lote y la interacción tiempo*lote

Minitab evalúa dos condiciones para determinar si existe una estimación significativa de la vida útil. En primer lugar, Minitab determina si la respuesta media se encuentra estadísticamente dentro de los límites de especificación.

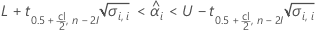
donde

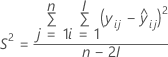
Término	Description
I	el número total de niveles de lote
n	el número total de valores de respuesta
X	la matriz de diseño para el modelo

En segundo lugar, Minitab determina si la respuesta media cambia a una tasa estadísticamente significativa con el tiempo.

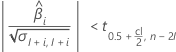
Si existe una estimación significativa, entonces Minitab determina si la respuesta media aumenta o disminuye con el tiempo. Si la segunda condición es falsa, entonces una de las siguientes condiciones es verdadera.

Si la respuesta disminuye con el tiempo, entonces Minitab calcula la vida útil en relación con el límite de especificación inferior. Esta fórmula da la condición cuando la respuesta disminuye:

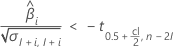
Si la respuesta aumenta con el tiempo, entonces Minitab calcula la vida útil en relación con el límite de especificación superior. Esta fórmula da la condición cuando la respuesta aumenta:

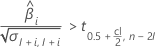
Si la respuesta media disminuye con el tiempo, entonces Minitab calcula la vida útil en relación con el límite de especificación inferior. De lo contrario, Minitab calcula la vida útil en relación con el límite de especificación superior.

Para obtener detalles sobre el cálculo de la vida útil en cada caso, vaya al tema correspondiente:

El modelo con tiempo y lote

Minitab evalúa dos condiciones para determinar si existe una estimación significativa de la vida útil. En primer lugar, Minitab determina si la respuesta media se encuentra estadísticamente dentro de los límites de especificación.

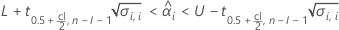
donde

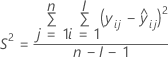
Término	Description
I	el número total de niveles de lote
n	el número total de valores de respuesta
X	la matriz de diseño para el modelo

En segundo lugar, Minitab determina si la respuesta media cambia a una tasa estadísticamente significativa con el tiempo.

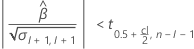
Si existe una estimación significativa, entonces Minitab determina si debe estimar la vida útil en relación con el límite de especificación superior o el límite de especificación inferior.

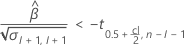
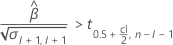
Para obtener detalles sobre el cálculo de la vida útil en cada caso, vaya al tema correspondiente:

El modelo con tiempo

Minitab evalúa dos condiciones para determinar si existe una estimación significativa de la vida útil. En primer lugar, Minitab determina si la respuesta media se encuentra estadísticamente dentro de los límites de especificación.

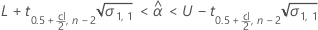
donde

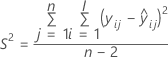
Término	Description
I	el número total de niveles de lote
n	el número total de valores de respuesta
X	la matriz de diseño para el modelo

En segundo lugar, Minitab determina si la respuesta media cambia a una tasa estadísticamente significativa con el tiempo.

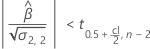
Si existe una estimación significativa, entonces Minitab determina si debe estimar la vida útil en relación con el límite de especificación superior o el límite de especificación inferior.

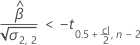
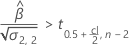
Para obtener detalles sobre el cálculo de la vida útil en cada caso, vaya al tema correspondiente:

Notación

Término	Description
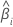	La pendiente para el iésimo lote
I	el número de niveles en el factor de lote
n	el número de filas en los datos
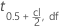	el valor de la distribución acumulada inversa a 0.5+cl/2 obtenido de la distribución t con df grados de libertad