En este tema
El modelo mixto y log-verosimilitud
La forma general del modelo mixto
Los modelos mixtos de los efectos contienen efectos fijos y aleatorios. La forma general del modelo mixto de los efectos es:
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
Notación
| Término | Description |
|---|---|
| y | el vector n x 1 de valores de respuesta |
| X | la matriz de diseño n x p para los efectos fijos, p ≤ n |
| Zi | la matriz de diseño n x mipara el iésimo efecto aleatorio en el modelo |
| β | un vector p x 1 de parámetros desconocidos |
| μi | un vector mi x 1 de variables independientes desde N(0, σ2i) |
| ε | un vector n x 1 de variables independientes desde N(0, σ2i) |
| c | el número de efectos aleatorios en el modelo |
Formas particulares del modelo mixto
Los estudios de estabilidad se ajustan a dos modelos con un factor de lote aleatorio. El modelo más grande contiene tiempo, el factor de lote aleatorio, y la interacción aleatoria entre tiempo y lote.
y = Xβ + Z1μ1+ Z2μ2 + ε
El modelo más pequeño contiene tiempo y el factor de lote aleatorio.
y = Xβ + Z1μ1+ε
La matriz general de varianzas-covarianzas del vector de respuesta, y, es:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
donde
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c se denominan componentes de la varianza.
Al factorizar a partir de la varianza, usted puede encontrar una representación de H(θ), que está en el cálculo de la log-verosimilitud de los modelos mixtos.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
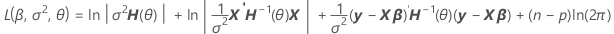
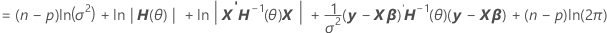
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| p | el número de parámetros en β, 2 para los estudios de estabilidad |
| σ2 | el componente de la varianza del error |
| X | la matriz de diseño ––para los términos fijos, la constante y el tiempo |
| H(θ) | In + θ1Z1Z'1 + ... + θcZcZ'c |
| In | la matriz de identidad con n filas y columnas |
| θi | la relación de la varianza del iésimo término aleatorio a la varianza del error |
| Zi | la matriz n x mi de codificaciones conocidas para el iésimo efecto aleatorio en el modelo |
| mi | el número de niveles para el iésimo efecto aleatorio |
| c | el número de efectos aleatorios en el modelo |
| |H(θ)| | el determinante de H(θ) |
| X' | la transpuesta de X |
| H-1(θ) | la inversa de H(θ) |
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 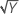 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Selección del modelo para lotes aleatorios
- Tiempo + Lote + Lote*Tiempo (pendientes e intersecciones diferentes para los lotes)
- Tiempo + Lote (pendientes iguales e intersecciones diferentes para los lotes)
- Tiempo (pendientes e intersecciones iguales para los lotes)
Si la interacción Lote*Tiempo es significativa, el análisis se ajusta al primer modelo. Si la interacción no es significativa, pero el término Lote es significativo en el segundo modelo, el análisis se ajusta el segundo modelo. De lo contrario, el análisis se ajusta al tercer modelo.
La prueba para determinar si se deben agrupar los lotes es ligeramente diferente de la prueba para incluir un lote, aunque ambas dependen de la distribución de chi-cuadrada. Las fórmulas para los estadísticos de prueba y los valores p son las siguientes.
Prueba entre el modelo 1 y el modelo 2
diferencia = −2L2 − (−2L1)
p = 0.5 * Prob(χ21 > diferencia) + 0.5 * Prob(χ22 > diferencia)
Prueba entre el modelo 2 y el modelo 3
diferencia = −2L3 − (−2L2)
p = 0.5 * Prob(χ21 > diferencia)
Notación
| Término | Description |
|---|---|
| La | la log-verosimilitud para el modelo a |
| p | el valor p para la prueba |
| Prob(χ21> diferencia) | la probabilidad de que una variable aleatoria de una distribución de chi-cuadrada con 1 grado de libertad es mayor que la diferencia |
| Prob(χ22> diferencia) | la probabilidad de que una variable aleatoria de una distribución de chi-cuadrada con 2 grados de libertad es mayor que la diferencia |
Referencias
- Searle, S.R. Casella, G. y McCuloch, C.E. (1992). Variance Components
- West, B.T., Welch, K.B. y Galecki, A.T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software.
- Chow, S. (2007). Statistical Design and Analysis of Stability Studies.
