En este tema
Valor ajustado
La y pronosticada o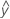 
; el valor de respuesta medio para los valores predictores dados utilizando la ecuación de regresión estimada.
Error estándar del valor ajustado marginal (EE ajuste)
El error estándar de los valores ajustados marginales en el modelo mixto depende del método de prueba para los efectos fijos. Para ambos métodos, los errores estándar son las raíces cuadradas de los elementos de la diagonal de la matriz de varianzas de los ajustes.
Método de Kenward-Roger
donde
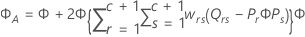
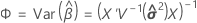
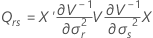
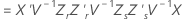
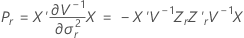
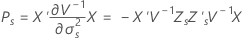
Aproximación de Satterthwaite
donde
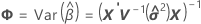
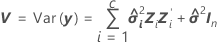
Residuos
Un residuo es la diferencia entre un valor observado y un valor ajustado. Esta parte de la observación no es explicada por el modelo ajustado. El residuo de una observación es:
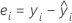
Cuando el lote es un factor aleatorio, Minitab calcula 2 tipos de residuos. Los residuos marginales utilizan el valor ajustado para un lote aleatorio, por lo que el coeficiente del lote no está en la ecuación.
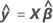
Los residuos condicionales utilizan el valor ajustado para un lote que está en los datos.
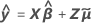
Notación
| Término | Description |
|---|---|
| yi | valor de la iésima respuesta observada |
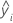 | iésimo valor de respuesta ajustado |
 | el vector de respuestas ajustadas |
| X | la matriz de diseño para los efectos fijos |
 | el vector de predictores fijos |
| Z | la matriz de diseño para los factores aleatorios |
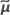 | el vector de los valores estimados de BLUP |
Residuos estandarizados
donde la desviación estándar de los residuos es la raíz cuadrada apropiada de la diagonal de la matriz de varianzas de los residuos:
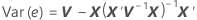
donde
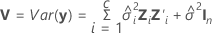
Notación
| Término | Description |
|---|---|
| ei | el iésimo residuo |
| Est.(ei) | la desviación estándar del iésimo residuo |
Intervalo de confianza
El rango en el que se espera que se encuentre la respuesta media estimada para un conjunto dado de valores predictores.
donde
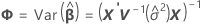
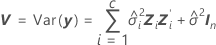
Los grados de libertad utilizan esta fórmula cuando el lote es un factor aleatorio:
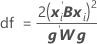
donde
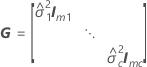
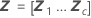
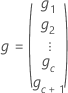
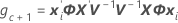
Notación
| Término | Description |
|---|---|
| t1-α/2, df | cuantil 1–α/2 de la distribución t con los grados de libertad dados |
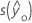 | error estándar del valor ajustado |
| X | matriz de diseño, incluyendo la constante |
| X' | transpuesta de X |
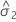 | componente de la varianza para el error |
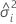 | componente de la varianza del iésimo factor aleatorio |
| Zi | matriz n x mi de codificaciones conocidas para el iésimo efecto aleatorio en el modelo |
| Zi' | transpuesta de Zi |
| In | matriz de identidad con n filas y columnas |
| xi | valores predictores para el ajuste o la predicción |
| W | matriz asintótica de varianzas-covarianzas del componente de la varianza para el error |
| c | número de efectos aleatorios en el modelo |
Intervalo de predicción
El rango en el que se espera que se encuentre la respuesta pronosticada para una nueva observación. El cálculo del intervalo de predicción depende de si el intervalo se calcula para el ajuste marginal o para el ajuste condicional.
Ajuste marginal
donde
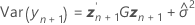
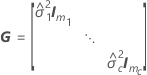
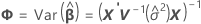
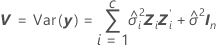
Los grados de libertad para el estadístico t vienen dados por esta fórmula:
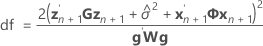
donde
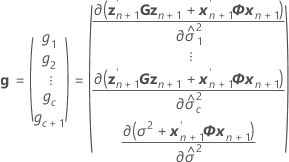
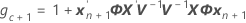
Ajuste condicional
donde
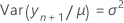
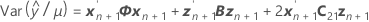
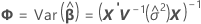
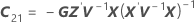
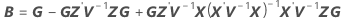
Los grados de libertad para el estadístico t son:
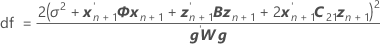
donde
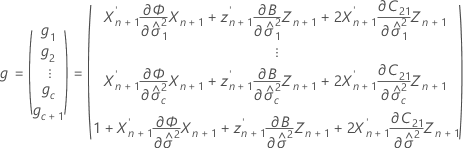
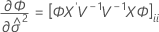
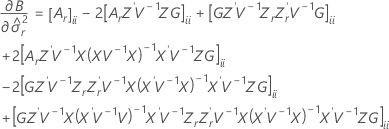
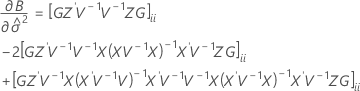
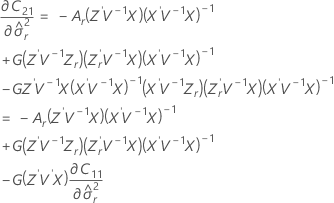
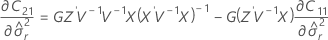
Notación
| Término | Description |
|---|---|
 | cuantil 1–α/2 de la distribución t con los grados de libertad dados |
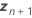 | vector de los nuevos valores de los predictores aleatorios |
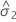 | componente de la varianza para el error |
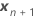 | vector de los nuevos valores de los predictores fijos |
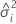 | componente de la varianza del iésimo factor aleatorio |
| Im | matriz de identidad con m filas y columnas |
| m | número de columnas de la matriz de diseño para representar el iésimo término aleatorio en el modelo |
| c | número de efectos aleatorios en el modelo |
| Zi | matriz de diseño n x mi para el iésimo efecto aleatorio en el modelo |
| Z'i | transpuesta de Zi |
