Suma de los cuadrados (SC)
En términos de matriz, estas son las fórmulas para las diferentes sumas de cuadrados:



Minitab desglosa el componente SC Regresión o SC Tratamientos en la cantidad de variación explicada por cada término utilizando tanto la suma de cuadrados secuenciales como la suma de cuadrados ajustados.
Notación
| Término | Description |
|---|---|
| b | vector de coeficientes |
| X | matriz de diseño |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| J | n entre n matriz de 1s |
CM ajust – Regresión
La fórmula del cuadrado medio (CM) de la regresión es:
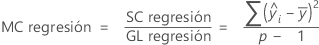
Notación
| Término | Description |
|---|---|
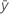 | respuesta media |
 | iésima respuesta ajustada |
| p | número de términos en el modelo |
CM ajustado – Error
El cuadrado medio del error (también abreviado como CM error o MSE y conocido como s2) es la varianza alrededor de la línea de regresión ajustada. La fórmula es:
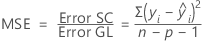
Notación
| Término | Description |
|---|---|
| yi | iésimo valor de respuesta observado |
 | iésima respuesta ajustada |
| n | número de observaciones |
| p | número de coeficientes en el modelo, sin contar la constante |
F
Si todos los factores en el modelo son fijos, entonces el cálculo del estadístico F depende de lo que se trata la prueba de hipótesis, como sigue:
- F(Término)
-

- F(Falta de ajuste)
-

Si hay factores aleatorios en el modelo, F se construye utilizando la información del cuadrado medio esperado para cada término. Para obtener más información, consulte a Neter et al.1.
Notación
| Término | Description |
|---|---|
| Término de CM Ajust. | Una medida de la cantidad de variación que explica un término después de representar los demás términos en el modelo. |
| Error CM | Una medida de la variación que el modelo no explica. |
| Falta de ajuste de CM | Una medida de la variación en la respuesta que pudiera modelarse agregando más términos al modelo. |
| Error puro CM | Una medida de la variación en los datos de respuesta replicada. |
- J. Neter, W. Wasserman y M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Valor p (P)
Se utilizan en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula. El valor p es la probabilidad de obtener un estadístico de prueba que sea por lo menos tan extremo como el valor real calculado, si la hipótesis nula es verdadera. Un valor de corte que se utiliza comúnmente para el valor p es 0.05. Por ejemplo, si el valor p calculado de un estadístico de prueba es menor que 0.05, usted rechaza la hipótesis nula.
