Seleccionar el modelo
Un ingeniero especializado en calidad que trabaja para un fabricante de medicamentos desea determinar la vida útil de un medicamento. La concentración del ingrediente activo en el medicamento disminuye con el tiempo. El ingeniero quiere determinar en qué momento la concentración alcanza 90% de la concentración prevista. El ingeniero selecciona de manera aleatoria 8 lotes de medicamentos de una población más grande de lotes posibles y prueba una muestra de cada lote en nueve momentos diferentes.
Para estimar la vida útil, el ingeniero realiza un estudio de estabilidad. Puesto que los lotes son una muestra aleatoria de una población más grande de lotes posibles, el lote es un factor aleatorio en lugar de un factor fijo.
- Abra los datos de muestra LotesAleatoriosVidaÚtil.MTW.
- Elija .
- En Respuesta, ingrese %Fármaco.
- En Tiempo, ingrese Mes.
- En Lote, ingrese Lote.
- En Espec. inferior, ingrese 90.
- Haga clic en Opciones.
- En la lista desplegable, seleccione El lote es un factor aleatorio.
- Haga clic en Aceptar y luego haga clic en Gráficas.
- En Gráficas de residuos, elija Cuatro en uno.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
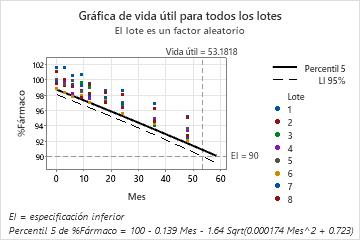
El valor p que compara los modelos con y sin la interacción de Mes por Lote es 0.059. Puesto que el valor p es menor que el nivel de significancia de 0.25, el análisis utiliza el modelo con la interacción de Mes por Lote. La vida útil, que es de aproximadamente 53 meses, es una estimación de por cuánto tiempo el ingeniero puede estar 95% seguro de que el 95% del fármaco está por encima del límite de especificación inferior. La estimación se aplica a cualquier lote que el ingeniero seleccione del proceso de manera aleatoria.
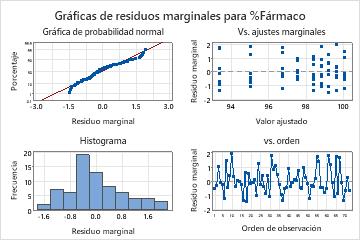
Es posible que los residuos marginales no sigan una distribución normal con varianza constante. Los puntos en la gráfica de probabilidad normal no siguen la línea adecuadamente. Una de las razones para el comportamiento no normal de los residuos marginales es que cuando el modelo final incluye la interacción de lote por tiempo, la varianza de los residuos marginales depende de la variable tiempo y no puede ser constante. Puede usar los residuos condicionales para verificar la normalidad del término de error en el modelo.
Información del factor
| Factor | Tipo | Número de niveles | Niveles |
|---|---|---|---|
| Lote | Aleatorio | 8 | 1, 2, 3, 4, 5, 6, 7, 8 |
Selección de modelo con α = 0.25
| Modelo | -2 logverosimilitud | Diferencia | Valor p |
|---|---|---|---|
| Mes Lote Mes*Lote | 128.599 | ||
| Mes Lote | 133.424 | 4.82476 | 0.059 |
Componentes de la varianza
| Fuente | Var | % del total | EE de la var. | Valor Z | Valor p |
|---|---|---|---|---|---|
| Lote | 0.527409 | 72.91% | 0.303853 | 1.735739 | 0.041 |
| Mes*Lote | 0.000174 | 0.02% | 0.000142 | 1.224102 | 0.110 |
| Error | 0.195739 | 27.06% | 0.036752 | 5.325932 | 0.000 |
| Total | 0.723322 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 0.442424 | 96.91% | 96.87% |
Coeficientes
| Término | Coef | EE del coef. | GL | Valor T | Valor p |
|---|---|---|---|---|---|
| Constante | 100.060247 | 0.268706 | 7.22 | 372.378347 | 0.000 |
| Mes | -0.138766 | 0.005794 | 7.22 | -23.950196 | 0.000 |
Predicciones de efectos aleatorios
| Término | BLUP | Desv.Est. | GL | Valor T | Valor p |
|---|---|---|---|---|---|
| Lote | |||||
| 1 | 1.359433 | 0.313988 | 12.45 | 4.329567 | 0.001 |
| 2 | 0.395375 | 0.313988 | 12.45 | 1.259203 | 0.231 |
| 3 | 0.109151 | 0.313988 | 12.45 | 0.347629 | 0.734 |
| 4 | -0.409322 | 0.313988 | 12.45 | -1.303623 | 0.216 |
| 5 | -0.135643 | 0.313988 | 12.45 | -0.432001 | 0.673 |
| 6 | -1.064736 | 0.313988 | 12.45 | -3.391006 | 0.005 |
| 7 | 0.049420 | 0.313988 | 12.45 | 0.157394 | 0.877 |
| 8 | -0.303678 | 0.313988 | 12.45 | -0.967164 | 0.352 |
| Mes*Lote | |||||
| 1 | 0.006281 | 0.008581 | 10.49 | 0.731925 | 0.480 |
| 2 | 0.019905 | 0.008581 | 10.49 | 2.319537 | 0.042 |
| 3 | -0.013831 | 0.008581 | 10.49 | -1.611742 | 0.137 |
| 4 | 0.003468 | 0.008581 | 10.49 | 0.404173 | 0.694 |
| 5 | 0.001240 | 0.008581 | 10.49 | 0.144455 | 0.888 |
| 6 | 0.000276 | 0.008581 | 10.49 | 0.032144 | 0.975 |
| 7 | -0.010961 | 0.008581 | 10.49 | -1.277272 | 0.229 |
| 8 | -0.006378 | 0.008581 | 10.49 | -0.743220 | 0.474 |
Ajustes y diagnósticos marginales para observaciones poco comunes
| Obs | %Fármaco | Ajuste | GL | Resid | Resid est. | |
|---|---|---|---|---|---|---|
| 10 | 101.564000 | 99.643950 | 7.04368 | 1.920050 | 2.375254 | R |
| 31 | 100.618000 | 98.811354 | 7.05273 | 1.806646 | 2.213787 | R |
| 55 | 98.481000 | 96.729866 | 8.87383 | 1.751134 | 2.033482 | R |
Cálculo de vida útil
Vida útil = período de tiempo en el que usted puede estar 95% seguro de que al menos 95% de
la respuesta está por encima del límite inferior de especificación
Vida útil para todos los lotes = 53.1818
Verificar los residuos condicionales
- Elija .
- Haga clic en Gráficas.
- En Residuos para gráficas, seleccione Condicional regular.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
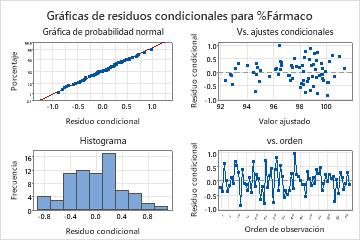
En estos resultados, los residuos condicionales parecen seguir una distribución normal. El modelo completo parece ajustarse adecuadamente a los datos.
