Ejemplo de Estudio de estabilidad con un factor de lote fijo

Un ingeniero especializado en calidad que trabaja para una empresa farmacéutica desea determinar la vida útil de píldoras que contienen un nuevo fármaco. La concentración del fármaco en las píldoras disminuye con el tiempo. El ingeniero quiere determinar en qué momento las píldoras alcanzan 90% de la concentración prevista. Puesto que se trata de un fármaco nuevo, la empresa solo cuenta con 5 lotes piloto para estimar la vida útil. El ingeniero prueba una píldora de cada lote en nueve momentos diferentes.

Para estimar la vida útil, el ingeniero realiza un estudio de estabilidad. Puesto que el ingeniero toma muestras de todos los lotes, el lote es un factor fijo en lugar de un factor aleatorio.

Abra los datos de muestra, VidaÚtil.MTW.
Elija Estadísticas > Regresión > Estudio de estabilidad > Estudio de estabilidad.
En Respuesta, escriba %Fármaco.
En Tiempo, escriba Mes.
En Lote, escriba Lote.
En Espec. inferior, ingrese 90.
Haga clic en Gráficas.
En Gráfica de vida útil, en la segunda lista desplegable, seleccione Sin gráficas para lotes individuales.
En Gráficas de residuos, seleccione Cuatro en uno.
Haga clic en Aceptar en cada cuadro de diálogo.

Interpretar los resultados

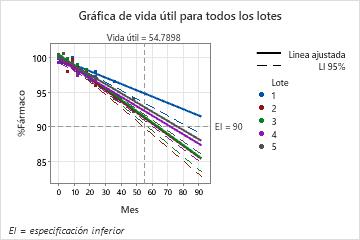
Para seguir las directrices de 2003 de la Conferencia Internacional sobre Armonización de Requisitos Técnicos para Registro de Productos Farmacéuticos de Uso Humano (ICH), el ingeniero selecciona un valor p de 0.25 para los términos que se incluirán en el modelo. El valor p de la interacción Mes por Lote es 0.048. Puesto que el valor p es menor que el nivel de significancia de 0.25, el ingeniero concluye que las pendientes de las ecuaciones de regresión para cada lote son diferentes. El lote 3 tiene la pendiente más pronunciada, -0.1630, lo que indica que la concentración disminuye más rápido en el lote 3. El lote 2 tiene la vida útil más corta, 54.79, por lo que la vida útil general es la vida útil del lote 2.

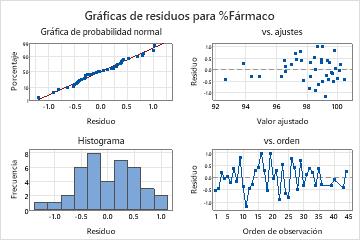
Los residuos son adecuadamente normales y están dispersados de forma aleatoria alrededor del 0. En la gráfica de residuos vs. ajustes, hay más puntos en el lado izquierdo de la gráfica que en el lado derecho. Este patrón se produce porque el ingeniero especializado en calidad recogió más datos al principio del estudio cuando las concentraciones eran altas. Este patrón no es una violación de los supuestos del análisis.

Fuente	GL	SC Sec.	MC sec.	Valor F	Valor p
Mes	1	122.460	122.460	345.93	0.000
Lote	4	2.587	0.647	1.83	0.150
Mes*Lote	4	3.850	0.962	2.72	0.048
Error	30	10.620	0.354
Total	39	139.516

Término	Coef	EE del coef.	Valor T	Valor p	FIV
Constante	100.085	0.143	701.82	0.000
Mes	-0.13633	0.00769	-17.74	0.000	1.07
Lote
1	-0.232	0.292	-0.80	0.432	3.85
2	0.068	0.292	0.23	0.818	3.85
3	0.394	0.275	1.43	0.162	3.41
4	-0.317	0.292	-1.08	0.287	3.85
5	0.088	0.275	0.32	0.752	*
Mes*Lote
1	0.0454	0.0164	2.76	0.010	4.52
2	-0.0241	0.0164	-1.47	0.152	4.52
3	-0.0267	0.0136	-1.96	0.060	3.65
4	0.0014	0.0164	0.08	0.935	4.52
5	0.0040	0.0136	0.30	0.769	*

Obs	%Fármaco	Ajuste	Resid	Resid est.
11	98.001	99.190	-1.189	-2.21	R
43	92.242	92.655	-0.413	-1.47		X
44	94.069	93.823	0.246	0.87		X

Lote	Vida útil
1	83.552
2	54.790
3	57.492
4	60.898
5	66.854
General	54.790

Ejemplo de Estudio de estabilidad con un factor de lote fijo

Interpretar los resultados

Método

Información del factor

Selección de modelo con α = 0.25

Resumen del modelo

Coeficientes

Ecuación de regresión

Ajustes y diagnósticos para observaciones poco comunes

Cálculo de vida útil

Lote
1	%Fármaco	=	99.853 - 0.0909 Mes

2	%Fármaco	=	100.153 - 0.1605 Mes

3	%Fármaco	=	100.479 - 0.1630 Mes

4	%Fármaco	=	99.769 - 0.1350 Mes

5	%Fármaco	=	100.173 - 0.1323 Mes