En este tema
Ecuación de regresión
Utilice la ecuación de regresión para describir la relación entre la respuesta y los términos en el modelo. La ecuación de regresión es una representación algebraica de la línea de regresión. La ecuación de regresión para el modelo lineal tiene la forma siguiente: Y= b0 + b1x1. En la ecuación de regresión, Y es la variable de respuesta, b0 es la constante o intersección, b1 es el coeficiente estimado para el término lineal (también denominado como pendiente de línea) y x1 es el valor del término.
La ecuación de regresión con más de un término toma la forma siguiente:
y = b0 + b1X1 + b2X2 + ... + bkXk
- y es la variable de respuesta
- b0 es la constante
- b1, b2, ..., bk son los coeficientes
- X1, X2, ..., Xk son los valores del término
Si el modelo contiene tanto variables continuas como categóricas, la tabla Ecuación de regresión puede mostrar una ecuación para cada combinación de niveles de las variables categóricas. Para utilizar estas ecuaciones para la predicción, debe elegir la ecuación correcta, con base en los valores de las variables categóricas y luego ingresar los valores de las variables continuas.
Valores de configuración de las variables
El modelo utiliza los valores de configuración de las variables para calcular las predicciones. Si los valores de las variables son poco comunes en comparación con los datos que Minitab usó para estimar el modelo, entonces Minitab muestra una advertencia debajo de la predicción.
Ajuste
Los valores ajustados también se conocen como ajustes o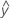 
. Los valores ajustados son estimaciones de punto de la respuesta media para los valores dados de los predictores. Los valores de los predictores también se conocen como valores de X.
Interpretación
Los valores ajustados se calculan ingresando los valores específicos de X para cada observación del conjunto de datos en la ecuación del modelo.
Por ejemplo, si la ecuación es y = 5 + 10x, el valor ajustado para el valor de X, 2, es 25 (25 = 5 + 10(2)).
Minitab advierte sobre predicciones con valores predictores poco comunes en comparación con los valores en los datos. Es necesario hacer más pruebas con muestras más antiguas para poder confirmar que la estimación de vida útil es exacta.
EE ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la respuesta media estimada para la configuración especificada de las variables. El cálculo del intervalo de confianza para la respuesta media utiliza el error estándar del ajuste. Los errores estándar siempre son no negativos.
Interpretación
Utilice el error estándar del ajuste para medir la precisión de la estimación de la respuesta media. Cuanto menor sea el error estándar, más precisa será la respuesta media pronosticada. Por ejemplo, un analista desarrolla un modelo para pronosticar el tiempo de entrega. Para un conjunto de valores de configuración de las variables, el modelo predice un tiempo medio de entrega de 3.80 días. El error estándar del ajuste para estos valores de configuración es 0.08 días. Para un segundo conjunto de valores de configuración de las variables, el modelo produce el mismo tiempo medio de entrega con un error estándar del ajuste de 0.02 días. El analista puede estar más seguro de que el tiempo medio de entrega del segundo conjunto de valores de configuración de las variables está cerca de 3.80 días.
Con el valor ajustado, usted puede utilizar el error estándar del ajuste para crear un intervalo de confianza para la respuesta media. Por ejemplo, dependiendo del número de grados de libertad, un intervalo de confianza de 95% se extiende aproximadamente dos errores estándar por encima y por debajo de la media pronosticada. Para los tiempos de entrega, el intervalo de confianza de 95% de la media pronosticada de 3.80 días cuando el error estándar es 0.08 es (3.64, 3.96) días. Usted puede estar 95% seguro de que la media de la población se encuentra dentro de este rango. Cuando el error estándar es 0.02, el intervalo de confianza de 95% es (3.76, 3.84) días. El intervalo de confianza del segundo conjunto de valores de configuración de las variables es más estrecho porque el error estándar es menor.
Intervalo de confianza para ajuste (IC de 95 %)
Estos intervalos de confianza (IC) son rangos de valores que probablemente contienen la respuesta media para la población que tiene los valores observados de los predictores o factores en el modelo.
Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si se toman muchas muestras, un determinado porcentaje de los intervalos de confianza resultantes incluirá el parámetro de población desconocido. El porcentaje de estos intervalos de confianza que contiene el parámetro es el nivel de confianza del intervalo.
El intervalo de confianza consta de las dos partes siguientes:
Interpretación
Utilice el intervalo de confianza para evaluar la estimación del valor ajustado para los valores observados de las variables.
Por ejemplo, con un nivel de confianza de 95 %, se puede estar un 95 % seguro de que el intervalo de confianza contiene la media de población para los valores especificados de los factores o variables predictoras en el modelo. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice el conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Un intervalo de confianza amplio indica que se puede estar menos seguro de la media de los valores futuros. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
IP de 95%
El intervalo de predicción es un rango que es probable que contenga una respuesta futura individual para una combinación seleccionada de valores de configuración de las variables. El intervalo de predicción siempre es más amplio que el intervalo de confianza correspondiente.
Interpretación
Por ejemplo, un ingeniero especializado en calidad determinó que la vida útil de un medicamento nuevo es 54.79 meses. La vida útil para este análisis se define como el momento en que el ingeniero ya no puede estar 95% seguro de que la concentración del peor lote es el 90% de la concentración prevista. El ingeniero desea predecir la concentración media para el peor lote a los 54.79 meses.
En estos resultados, la predicción de la respuesta media es aproximadamente 91.36%. Sin embargo, el ingeniero también quiere estimar el rango de valores para una sola píldora del lote 2. El intervalo de predicción indica que usted puede estar 95% seguro de que la concentración pronosticada para una sola píldora del lote 2 a los 54.79 meses está entre aproximadamente 89.3217% y 93.4001%.
Configuración
| Variable | Valor de configuración |
|---|---|
| Mes | 54.79 |
| Lote | 2 |
Predicción
| Ajuste | EE de ajuste | IC de 95% | IP de 95% | |
|---|---|---|---|---|
| 91.3609 | 0.801867 | (89.7233, 92.9986) | (89.3217, 93.4001) | XX |
