En este tema
Coeficientes y coeficientes estandarizados
Los coeficientes son los parámetros en una ecuación de regresión. Los coeficientes estimados se utilizan con los predictores para calcular el valor ajustado de la variable de respuesta y la respuesta pronosticada de nuevas observaciones. A diferencia de los mínimos cuadrados, los coeficientes de PLS son estimadores no lineales. Los coeficientes estandarizados indican la importancia de cada predictor en el modelo y corresponden a las variables X y Y estandarizadas. En PLS, la matriz de coeficientes (dimensión p × r) se calcula a partir de las ponderaciones y las influencias.
La fórmula para los coeficientes estandarizados es:

Para calcular los coeficientes no estandarizados y la intersección, utilice estas fórmulas:
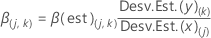

Notación
| Término | Description |
|---|---|
| W | la matriz de ponderaciones de X |
| P | la matriz de influencias de X |
| C | la matriz de influencias de Y |
| j | los predictores (1, p) |
| k | las respuestas (1, r) |
| p | el número de predictores |
| r | el número de respuestas |
Apalancamientos
En la regresión de mínimos cuadrados, los apalancamientos son valores que indican qué tan lejos están las observaciones correspondientes del centro del espacio X, que es descrito por los valores de X. En PLS, los predictores son reemplazados por las puntuaciones de X. Las observaciones con un alto apalancamiento tienen puntuaciones de X alejadas de cero y tienen influencias significativas en los coeficientes de regresión. Los puntos con un alto apalancamiento son valores atípicos en el espacio X, pero no son necesariamente valores atípicos en el espacio Y.
Los valores de apalancamiento en PLS se calculan a partir de la matriz T de puntuaciones de X, que se utiliza para calcular la matriz de sombrero (H) de la siguiente manera:

El apalancamiento (hii) de la iésima observación es el iésimo elemento diagonal de la matriz H.
Un valor de apalancamiento mayor que 2m / n se considera alto y se debe examinar.
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| m | el número de componentes |
Distancias con respecto al modelo X
Una medida de qué tan bien se ajustan las observaciones en el espacio X; indica qué tan bien son descritas las observaciones por las puntuaciones de X. Una observación con una distancia grande también puede ser también un punto de apalancamiento.
Fórmula
La fórmula para calcular la distancia desde el modelo X para la iésima observación es:
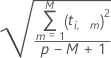
Notación
| Término | Description |
|---|---|
| M | número de componentes |
| t | puntuación de X |
| p | número de predictores |
Distancias con respecto al modelo Y
Una medida de qué tan bien se ajustan las observaciones en el espacio Y; indica qué tan bien son descritas las observaciones por las puntuaciones de Y. Una observación con un valor de distancia grande también pudiera ser un valor atípico.
Fórmula
La siguiente es la fórmula para calcular la distancia con respecto al modelo Y para la iésima observación:
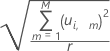
Notación
| Término | Description |
|---|---|
| M | el número de componentes |
| u | la puntuación de Y |
| r | el número de respuestas |
