En este tema
Puntuaciones de X
Las puntuaciones de X son combinaciones lineales de los términos, similares a las puntuaciones de los componentes principales. Las puntuaciones de X forman una matriz n × m de columnas no correlacionadas. Las puntuaciones de X son proyecciones de las observaciones en los componentes de PLS. PLS ajusta las puntuaciones de X, que reemplazan a los términos originales en los datos, utilizando la estimación de cuadrados mínimos.
Fórmula
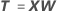
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| m | el número de componentes |
| i | las observaciones desde 1 hasta n |
| j | los términos desde 1 hasta p |
| X | la matriz de diseño |
| W | la matriz de ponderaciones de X |
Influencias de X
Las influencias de X son coeficientes lineales que vinculan los términos a las puntuaciones de X; similar a los vectores propios en el análisis de componentes principales. Los valores de influencia indican la importancia del término correspondiente para el componente mésimo. Las influencias de X forman una matriz p × m.
Fórmula
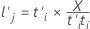
Notación
| Término | Description |
|---|---|
| p | el número de términos |
| m | el número de componentes |
| i | las observaciones desde 1 hasta n |
| j | los términos desde 1 hasta p |
| t | las puntuaciones de X |
| X | los predictores |
Ponderaciones de X
Las ponderaciones de X describen la covarianza entre los términos y las respuestas. En el algoritmo, las ponderaciones aseguran que las puntuaciones de X sean ortogonales, o no estén relacionadas entre sí, y se utilizan para calcular las puntuaciones de X. Las ponderaciones de X forman una matriz de p × m.
Fórmula
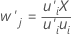
Minitab escala el vector de ponderaciones para que la longitud del vector sea 1.
Notación
| Término | Description |
|---|---|
| p | el número de términos |
| m | el número de componentes |
| i | las observaciones desde 1 hasta n |
| j | los términos desde 1 hasta p |
| X | la matriz de residuos de X |
| u | las puntuaciones de Y |
Residuos de X
Los residuos de X contienen la varianza en los predictores que no es explicada por el modelo PLS. Las observaciones con residuos de X relativamente grandes son valores atípicos en el espacio X, lo que indica que no son explicadas adecuadamente por el modelo.
Los residuos de X son las diferencias entre los valores predictores reales y los valores calculados de X y están en la misma escala que los predictores originales. La matriz de residuos de X, similar a la matriz original de X, es una matriz n x p.
La matriz de residuos de X se establece inicialmente en la matriz estandarizada de X. Después de calcular el componente mésimo y obtener el vector de puntuaciones de X y el vector de influencias de X, Minitab calcula los residuos de X.
Fórmula

Minitab luego calcula los residuos no estandarizados de X multiplicando los residuos estandarizados de X por la desviación estándar de los valores predictores.
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| p | el número de términos |
| i | las observaciones desde 1 hasta n |
| j | los términos desde 1 hasta p |
| t | las puntuaciones de X |
| l | las influencias de X |
Valores calculados de X
Los valores calculados de X son combinaciones lineales de las puntuaciones de X; contienen la varianza en los predictores explicada por el modelo PLS. Las observaciones con valores calculados de X relativamente pequeños son valores atípicos en el espacio X y el modelo no los explica adecuadamente.
La matriz calculada de X, similar a la matriz original de X, es una matriz n x p, donde n es igual al número de observaciones y p es igual al número de predictores. Los valores calculados de X están en la misma escala que los predictores.
La matriz calculada de X se inicializa en la matriz de ceros. Después de calcular el componente mésimo y obtener el vector de puntuaciones de X y el vector de influencias de X, Minitab calcula los valores calculados de X. Si el número de componentes es igual al número de predictores, entonces el valor calculado de X es igual al valor original de X.
Fórmula
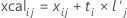
Minitab luego calcula los valores calculados de X no estandarizados multiplicando los valores calculados de X estandarizados por la desviación estándar de los valores predictores y sumando la media.
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| p | el número de predictores |
| i | el número de observaciones desde 1 hasta n |
| j | el número de predictores desde 1 hasta p |
| t | las puntuaciones de X |
| l | las influencias de X |
Puntuaciones de Y
Las puntuaciones de Y son combinaciones lineales de las variables de respuesta. Las puntuaciones de Y forman una matriz de n × m. Las puntuaciones de Y son proyecciones de las observaciones en los componentes de PLS.
Fórmula
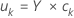
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| m | el número de componentes |
| k | el número de respuestas desde 1 hasta r |
| Y | la matriz de Y |
| c | las influencias de Y |
Influencias de Y
Las influencias de Y son los coeficientes lineales que vinculan las respuestas a las puntuaciones de Y. Los valores de influencia indican la importancia de la respuesta correspondiente para el componente mésimo. Las influencias de Y forman una matriz de r × m.
Fórmula

Notación
| Término | Description |
|---|---|
| r | el número de respuestas |
| m | el número de componentes |
| i | las observaciones desde 1 hasta n |
| k | las respuestas desde 1 hasta r |
| Y | las respuestas |
| t | las puntuaciones de X |
Residuos de Y
Los residuos de Y contienen la varianza restante en las respuestas que no es explicada por el modelo PLS. Las observaciones con residuos de Y relativamente grandes son valores atípicos en el espacio Y, lo que indica que no son explicadas adecuadamente.
Los residuos de Y son las diferencias entre los valores de respuesta reales y los valores calculados de Y, y se encuentran en la misma escala que las respuestas originales. La matriz de residuos de Y, similar a la matriz original de Y, es una matriz n x r.
La matriz de residuos de Y se establece inicialmente en la matriz estandarizada de Y. Después de calcular el componente mésimo y obtener los ventores de puntuación de X e influencia de Y, Minitab determina los residuos estandarizados de Y.
Fórmula

Minitab luego calcula los residuos no estandarizados de Y multiplicando los residuos estandarizados de Y por la desviación estándar de los valores de respuesta correspondientes.
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| r | el número de respuestas |
| i | las observaciones desde 1 hasta n |
| k | las respuestas desde 1 hasta r |
| t | las puntuaciones de X |
| c | las influencias de Y |
Valores calculados de Y
Los valores calculados de Y son combinaciones lineales de las puntuaciones de X; contienen la varianza en las respuestas explicadas por el modelo PLS. Las observaciones con valores calculados de Y relativamente pequeños son valores atípicos en el espacio Y no son explicadas adecuadamente.
La matriz calculada de Y, al igual que la matriz original de Y, es una matriz n x r. La matriz calculada de Y se estable inicialmente en la matriz cero. Después de que Minitab calcula el mésimo componente y obtiene los vectores de puntuación de X e influencia de Y, Minitab determina los valores calculados de Y estandarizados.
Fórmula
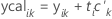
Minitab luego calcula los valores calculados de Y no estandarizados multiplicando los valores calculados de Y estandarizados por la desviación estándar de la respuesta correspondiente y sumando la media.
Notación
| Término | Description |
|---|---|
| n | el número de observaciones |
| r | el número de respuestas |
| i | las observaciones desde 1 hasta n |
| k | las respuestas desde 1 hasta r |
| t | las puntuaciones de X |
| c | las influencias de Y |
