Ajustes
Los valores ajustados también se conocen como ajustes o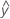 
. Los valores ajustados son estimaciones de punto de la respuesta media para los valores dados de los predictores. Los valores de los predictores también se conocen como valores de X.
Interpretación
Los valores ajustados se calculan ingresando los valores específicos de X para cada observación del conjunto de datos en la ecuación del modelo.
Por ejemplo, si la ecuación es y = 5 + 10x, el valor ajustado para el valor de X, 2, es 25 (25 = 5 + 10(2)).
EE ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la respuesta media estimada para la configuración especificada de las variables. El cálculo del intervalo de confianza para la respuesta media utiliza el error estándar del ajuste. Los errores estándar siempre son no negativos.
Interpretación
Utilice el error estándar del ajuste para medir la precisión de la estimación de la respuesta media. Cuanto menor sea el error estándar, más precisa será la respuesta media pronosticada. Por ejemplo, un analista desarrolla un modelo para pronosticar el tiempo de entrega. Para un conjunto de valores de configuración de las variables, el modelo predice un tiempo medio de entrega de 3.80 días. El error estándar del ajuste para estos valores de configuración es 0.08 días. Para un segundo conjunto de valores de configuración de las variables, el modelo produce el mismo tiempo medio de entrega con un error estándar del ajuste de 0.02 días. El analista puede estar más seguro de que el tiempo medio de entrega del segundo conjunto de valores de configuración de las variables está cerca de 3.80 días.
Con el valor ajustado, usted puede utilizar el error estándar del ajuste para crear un intervalo de confianza para la respuesta media. Por ejemplo, dependiendo del número de grados de libertad, un intervalo de confianza de 95% se extiende aproximadamente dos errores estándar por encima y por debajo de la media pronosticada. Para los tiempos de entrega, el intervalo de confianza de 95% de la media pronosticada de 3.80 días cuando el error estándar es 0.08 es (3.64, 3.96) días. Usted puede estar 95% seguro de que la media de la población se encuentra dentro de este rango. Cuando el error estándar es 0.02, el intervalo de confianza de 95% es (3.76, 3.84) días. El intervalo de confianza del segundo conjunto de valores de configuración de las variables es más estrecho porque el error estándar es menor.
IC de 95%
El intervalo de confianza para el ajuste proporciona un rango de valores probables para la respuesta media dada la configuración especificada de los predictores.
Interpretación
Utilice el intervalo de confianza para evaluar la estimación del valor ajustado para los valores observados de las variables.
Por ejemplo, con un nivel de confianza de 95%, usted puede estar 95% seguro de que el intervalo de confianza contiene la media de la población para los valores especificados de las variables incluidas en el modelo. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Un intervalo de confianza amplio indica que usted puede estar menos seguro acerca de la media de los valores futuros. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
IP de %95
El intervalo de predicción es un rango que es probable que contenga una respuesta futura individual para un valor de la variable predictora.
Interpretación
Con el intervalo de predicción de 95%, usted puede estar 95% seguro de que las nuevas observaciones estarán dentro del intervalo. (Sin embargo, tenga en cuanta que esto solo es válido para los valores que están incluidos dentro del rango de los datos en el análisis.) El intervalo se define por los límites inferior y superior, que se calculan a partir del nivel de confianza y el error estándar de la predicción. El intervalo de predicción siempre es más amplio que el intervalo de confianza debido a la incertidumbre adicional que implica la predicción de una respuesta individual en comparación con la respuesta media.
R-cuad. de prueba
El R2 de prueba representa la proporción de la variación en las respuestas que es explicada por el modelo original utilizando los valores predictores de los datos de prueba.
El conjunto de datos de prueba debe incluir el mismo número de predictores que el conjunto de datos original. El R2 de prueba solo se puede calcular si los datos de prueba incluyen datos de respuesta para cada observación. El R2 de prueba se calcula de la misma manera que el R2.
Interpretación
El R2 de prueba identifica hasta qué punto el modelo de regresión de PLS predice sus datos de prueba. Valores mayores de R2 de prueba indican que el modelo tiene una mayor capacidad de predicción.
A menudo, la regresión de PLS es realizada en dos pasos. El primer paso, denominado algunas veces capacitación, supone el cálculo de un modelo de regresión de PLS para un conjunto de datos de muestra (también denominado conjunto de datos de capacitación). El segundo paso incluye la comprobación de este modelo con un conjunto de datos diferente, denominado a menudo conjunto de datos de prueba. Algunos conjuntos de datos de prueba contienen valores de respuestas, otros no.. Si el conjunto de datos de prueba incluye valores de respuesta, entonces Minitab podrá calcular una prueba R2.
Si utiliza validación cruzada, compare la prueba R2 con el R2-cuadrado pronosticado. Lo ideal es que estos valores sean similares. Una prueba R2 que es significativamente más pequeña que el R2 pronosticado indica que la validación cruzada es muy optimista acerca de la capacidad de predicción del modelo o que las dos muestras de datos pertenecen a poblaciones diferentes.
