En este tema
Gráfica de selección del modelo
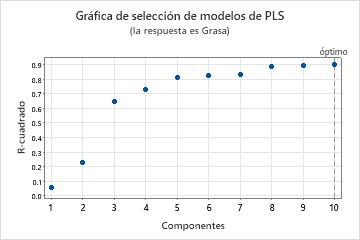
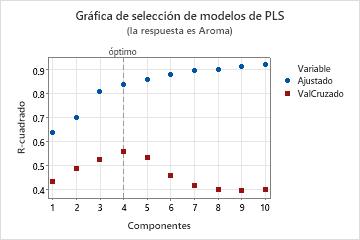
La gráfica de selección del modelo es una gráfica de dispersión de los valores de R2 y R2 pronosticado en función del número de componentes que se ajustan o a los que se aplica validación cruzada. Es una representación gráfica de la tabla Selección y validación del modelo. Si usted no utiliza validación cruzada, los valores de R2 pronosticado no aparecen en la gráfica. Minitab provee una gráfica de selección del modelo por cada respuesta.
Interpretación
Utilice esta gráfica para comparar la potencia de caracterización y predicción de diferentes modelos para determinar el número apropiado de componentes que se deben conservar en el modelo. La línea vertical en la gráfica indica el número de componentes que Minitab seleccionó para el modelo PLS.
Gráfica de respuesta
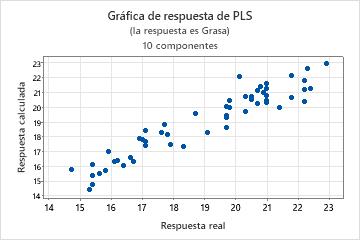
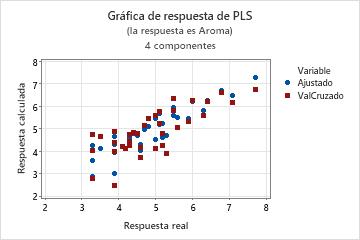
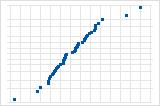
La gráfica de respuesta es una gráfica de dispersión de los valores ajustados versus las respuestas reales. Si usted realiza una validación cruzada, la gráfica también incluye los valores ajustados versus los valores ajustados con validación cruzada. Minitab proporciona una gráfica de respuesta por cada respuesta.
Interpretación
- Un patrón no lineal en los puntos, que indica que el modelo no puede ajustarse ni predecir los datos adecuadamente.
- Si realiza una validación cruzada, diferencias grandes en los valores ajustados y los valores ajustados con validación cruzada, que indican un punto de apalancamiento.
Un modelo con excelente capacidad predictiva por lo general tiene una pendiente de 1 e intersecta el eje Y en 0.
Gráfica de coeficientes
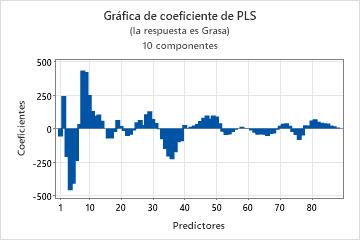
La gráfica de coeficientes es una gráfica de dispersión proyectada que muestra coeficientes no estandarizados para cada predictor. Minitab ofrece una gráfica de coeficientes por cada respuesta.
Interpretación
Utilice la gráfica de coeficientes, junto con la salida de coeficientes de regresión para comparar el signo y la magnitud de los coeficientes para cada predictor. La gráfica permite identificar rápidamente los predictores que son más o menos importantes en el modelo.
Puesto que la gráfica muestra coeficientes no estandarizados, usted solo puede hacer comparaciones de la magnitud de las relaciones entre los predictores y la respuesta si los predictores están en la misma escala (por ejemplo, datos espectrales). De lo contrario, utilice la gráfica de coeficientes estandarizados o la gráfica de influencias para comparar las ponderaciones de los predictores utilizados para calcular los componentes.
Gráfica de coeficientes estandarizados
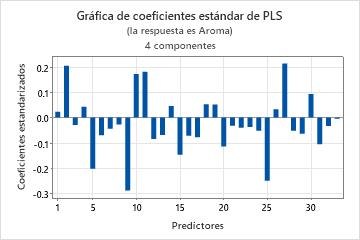
La gráfica de coeficientes es una gráfica de dispersión proyectada que muestra los coeficientes estandarizados para cada predictor. Minitab ofrece una gráfica de coeficientes estandarizados por cada respuesta.
Interpretación
Utilice esta gráfica, junto con la salida de coeficientes de regresión para comparar el signo y la magnitud de los coeficientes para cada predictor. La gráfica permite identificar rápidamente los predictores que son más o menos importantes en el modelo.
Debido a que la gráfica muestra los coeficientes estandarizados, usted puede comparar la magnitud de las relaciones entre los predictores y la respuesta, incluso si los predictores no están en la misma escala.
Si los predictores están en la misma escala, el patrón de coeficientes en las gráficas estandarizada y no estandarizada tienen una apariencia similar. Sin embargo, estas gráficas podrían no tener la misma apariencia debido a que los predictores están muy correlacionados, lo que hace que los coeficientes sean inestables, y debido a las diferencias entre las desviaciones estándar de las muestras y las desviaciones estándar de las poblaciones.
Gráfica de distancia
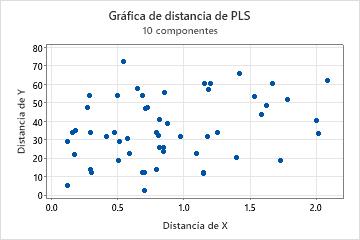
La gráfica de distancia es una gráfica de dispersión de la distancia de cada observación con respecto al modelo X y Y. Las distancias con respecto al modelo Y miden qué tan bien se ajusta una observación en el espacio Y. Las distancias con respecto al modelo X miden qué tan bien se ajusta una observación el espacio X.
Interpretación
Cuando examine esta gráfica, busque los puntos con distancias mayores que otros puntos en los ejes X y Y. Las observaciones con distancias más grandes con respecto al modelo Y pueden ser valores atípicos y las observaciones con distancias más grandes con respecto al modelo X pueden ser puntos de apalancamiento.
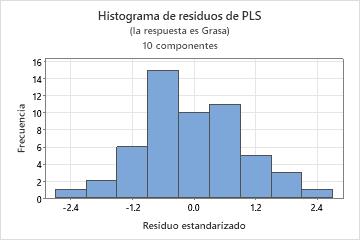
Histograma de residuos
El histograma de los residuos estandarizados muestra la distribución de los residuos estandarizados para todas las observaciones.
Interpretación
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Una cola larga en una dirección | Asimetría |
| Una barra que está muy alejada de las otras barras | Un valor atípico |
Puesto que el aspecto de un histograma depende del número de intervalos utilizados para agrupar los datos, no utilice un histograma para evaluar la normalidad de los residuos. En lugar de ello, utilice una gráfica de probabilidad normal. Un histograma es más efectivo cuando usted tiene aproximadamente 20 o más puntos de datos. Si la muestra es demasiado pequeña, entonces cada barra del histograma no contiene suficientes puntos de datos para revelar asimetría o valores atípicos de una manera fiable.
Gráfica de probabilidad normal de los residuos
La gráfica de probabilidad normal de los residuos muestra los residuos estandarizados en función de sus valores esperados cuando la distribución es normal.
Interpretación
Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
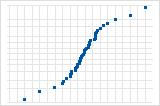
La curva S implica una distribución con colas largas.
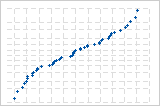
La curva S invertida implica una distribución con colas cortas.
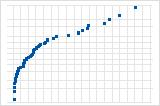
La curva descendente implica una distribución con asimetría a la derecha.
Algunos puntos alejados de la línea implican una distribución con valores atípicos.
Si observa un patrón no normal, utilice las otras gráficas de residuos para verificar otros problemas con el modelo, como términos faltantes o un efecto del orden cronológico. Si los residuos no siguen una distribución normal, los intervalos de confianza y los valores p pueden ser inexactos.
Residuos vs. ajustes
La gráfica de residuos vs. ajustes representa los residuos estandarizados en el eje Y los valores ajustados en el eje X.
Interpretación
Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
| Un punto que está lejos de los otros puntos en la dirección x | Un punto influyente |

Gráfica con valor atípico
Uno de los puntos es mucho más grande que todos los otros puntos. Por lo tanto, el punto es un valor atípico. Si hay demasiados valores atípicos, el modelo podría no ser aceptable. Usted debe tratar de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). A continuación, repita el análisis.
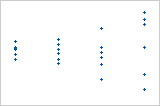
Gráfica con varianza no constante
La varianza de los residuos aumenta con los valores ajustados. Tenga en cuenta que, a medida que el valor de los ajustes aumenta, la dispersión entre los residuos se amplía. Este patrón indica que las varianzas de los residuos son desiguales (no constante).
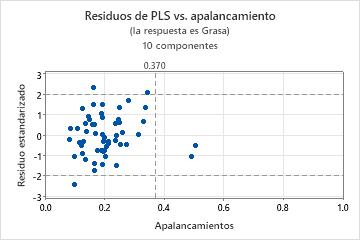
Gráfica de residuos vs. apalancamiento
La gráfica de residuos vs. apalancamiento es una gráfica de dispersión de los residuos estandarizados versus el apalancamiento de cada observación.
Interpretación
- Valores atípicos: Observaciones con residuos estandarizados mayores que +/- 2, las cuales se encuentran fuera de las líneas horizontales de referencia de la gráfica.
- Puntos de apalancamiento: Observaciones con valores de apalancamiento mayores que 2m / n, donde m = número de componentes y n = número de observaciones, que se consideran extremas. Tienen puntuaciones de X distantes del cero y se encuentran a la derecha de la línea vertical de referencia, que se encuentra en el valor 2m / n en el eje X. Si 2m / n es mayor que uno, la línea de referencia no aparece en la gráfica debido a que los valores de apalancamiento siempre están entre 0 y 1.
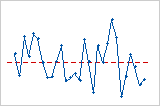
Residuos vs. orden
La gráfica de residuos versus orden muestra los residuos estandarizados en el orden en que se recopilaron los datos.
Interpretación
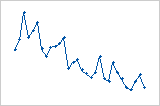
Tendencia
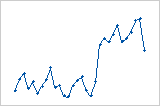
Cambio
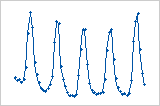
Ciclo
Gráfica de puntuaciones
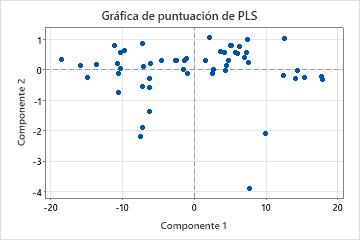
La gráfica de puntuaciones es una gráfica de dispersión de las puntuaciones de X del primer componente y el segundo componente incluidos en el modelo.
Interpretación
Si los dos primeros componentes explican la mayorparte de la varianza en los predictores, entonces la configuración de los puntos en esta gráfica refleja fielmente la configuración multidimensional original de los datos. Para verificar qué tanto de la varianza en los predictores es explicada por el modelo, examine los valores de varianza de X en la tabla Selección y validación del modelo. Si el valor de varianza de X es alto, el modelo explica la varianza en la significancia de los predictores.
- Puntos de apalancamiento: Los puntos que se encuentran lejos de la mayoría de los puntos en la gráfica pueden ser puntos de apalancamiento y podrían tener un efecto significativo en los resultados.
- Conglomerados: Los puntos que forman grupos pueden indicar dos o más distribuciones separadas en los datos, las cuales podrían ser descritas de mejor forma por modelos diferentes.
Nota
Si el modelo contiene más de 2 componentes, convendría graficar las puntuaciones de X de otros componentes utilizando una Gráfica de dispersión. Para ello, almacene la matriz de puntuaciones de X y, a continuación, copie la matriz en columnas utilizando . Si el modelo solo tiene un componente, esta gráfica no aparece en la salida.
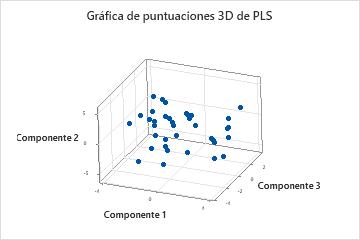
Gráfica de puntuación 3D
La gráfica de puntuaciones 3D es una gráfica de dispersión tridimensional de las puntuaciones de X a partir de los componentes primero, segundo y tercero del modelo. Si los tres primeros componentes explican la mayor parte de la varianza en los predictores, entonces la configuración de los puntos en esta gráfica refleja fielmente la configuración multidimensional original de los datos. Para verificar cuánta varianza explica el modelo, examine los valores de varianza de X en la tabla Selección y validación del modelo. Si el valor de varianza de X es alto, el modelo explica la varianza en la significancia de los predictores.
Interpretación
- Puntos de apalancamiento: Los puntos que se encuentran lejos de la mayoría de los puntos en la gráfica pueden ser puntos de apalancamiento y podrían tener un efecto significativo en los resultados.
- Conglomerados: Los puntos que forman grupos pueden indicar dos o más distribuciones separadas en los datos, las cuales podrían ser descritas de mejor forma por modelos diferentes.
También debería utilizar las herramientas de la gráfica 3D, que permiten rotar la gráfica para que se pueda observar desde perspectivas diferentes. Esto le ofrecerá una vista más completa de sus datos, además de permitirle identificar más adecuadamente los puntos de apalancamiento y los conglomerados de puntos.
Gráfica de influencias
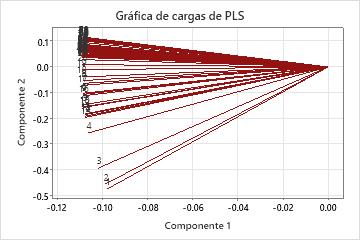
La gráfica de influencias es una gráfica de dispersión de los predictores proyectados sobre los componentes primero y segundo del modelo. Muestra las influencias de X para el segundo componente graficadas en función de las influencias de X del primer componente. Cada punto, que representa un predictor, está conectado a (0,0) en la gráfica.
Interpretación
La gráfica de influencias muestra qué tan importantes son los predictores para los dos primeros componentes, además de ser particularmente útil cuando los predictores se encuentran en escalas diferentes. Si los componentes explican la mayor parte de la varianza de X, que se muestra en la tabla Selección y validación del modelo, entonces la gráfica de influencias indica qué tan importantes son los predictores en el espacio X. Cuando considere la importancia de los predictores en todo el modelo, también debe considerar cuánta varianza explican los componentes en las respuestas. Para verificar esto, examine los valores de R2 y R2 pronosticado en la tabla Selección y validación del modelo.
- Ángulos entre las líneas, que representan la correlación entre predictores. Ángulos más pequeños indican que los predictores están muy correlacionados.
- Predictores con líneas más largas, que tienen mayores influencias en los componentes primero y segundo y son más importantes en el modelo.
Nota
Si el modelo contiene más de 2 componentes, convendría graficar las influencias de X de otros componentes utilizando una Gráfica de dispersión. Para ello, almacene la matriz de influencias de X y, a continuación, copie la matriz en columnas utilizando .
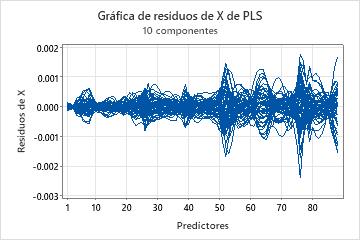
Gráfica de residuos de X
La gráfica de residuos de X es una gráfica de línea de los residuos de X versus los predictores. Cada línea representa una observación y tiene tantos puntos como predictores.
Interpretación
Utilice la gráfica de matriz de los residuos de X para identificar observaciones o predictores que el modelo describe deficientemente. Esta gráfica es más útil con predictores que se encuentran en la misma escala.
- Cuando las líneas estén separadas en el mismo punto del eje X, el modelo describe deficientemente el predictor en ese punto.
- Cuando una línea de la gráfica se desvía de las otras líneas, el modelo describe deficientemente la observación representada por esa línea.
Utilice la gráfica de matriz de residuos de X para examinar patrones generales en los residuos e identificar áreas donde existan problemas. Posteriormente, examine los residuos de X que se muestren en la salida para determinar las observaciones y los predictores que el modelo describe deficientemente.
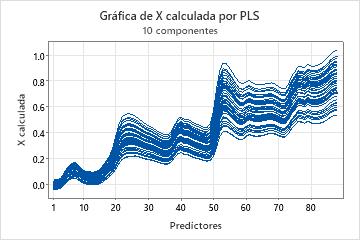
Gráfica de X calculada
La gráfica de X calculada es una gráfica de línea de los valores calculados de X versus los predictores. Cada línea representa una observación y tiene tantos puntos como predictores.
Interpretación
Utilice esta gráfica para identificar observaciones o predictores que el modelo describe deficientemente. Esta gráfica es más útil con predictores que se encuentran en la misma escala.
La gráfica de X calculada complementa la gráfica de residuos de X. La suma de ambas gráficas produce una gráfica de los valores predictores originales. Un predictor con valores calculados de X que son mucho más pequeños o grandes que los valores originales de X no es descrito adecuadamente por el modelo.