En este tema
Función de enlace
Minitab ofrece tres funciones de enlace: logit (la predeterminada), normit y gompit. Las funciones de enlace permiten ajustar una amplia clase de modelos de respuesta ordinal. El logit es la inversa de la función de distribución logística acumulada estándar. La función normit, también conocida como probit, es la inversa de la función de distribución normal acumulada estándar. La función gompit, también conocida como log-log complementario, es la inversa de la función de distribución de Gompertz.
Fórmula
g(χk) = θk +x'β, k = 1, ..., K-1
La función de enlace es la inversa de una función de distribución. Las funciones de enlace y sus distribuciones correspondientes se resumen a continuación:
| Nombre | Función de enlace | Distribución |
|---|---|---|
| logit | g(χ) = loge(χ/ (1 – χ)) | logística |
| normit (probit) |
g(χ) = Φ–1(χ) |
normal |
| gompit (log-log complementario) | g(χ) =loge (–loge(1 – χ)) | Gompertz |
Notación
| Término | Description |
|---|---|
| K | número de categorías distintas en la respuesta |
| χk | probabilidad acumulada hasta e incluyendo la categoría k, (π1+ ...+ πk) |
| g(χk) | vector de variables predictoras |
| θk | constante asociada con la késima categoría de respuesta distinta |
| x | un vector de variables predictoras |
| β | un vector de coeficientes asociados con los predictores |
Patrón de factor/covariable
Describe un conjunto individual de valores de factor/covariable en un conjunto de datos. Minitab calcula las probabilidades del evento, los residuos y otras medidas de diagnóstico para cada patrón de factor/covariable.
Por ejemplo, si un conjunto de datos incluye los factores sexo y raza y la covariable edad, la combinación de estos predictores puede contener tantos patrones diferentes de covariables como sujetos. Si un conjunto de datos solamente incluye los factores raza y sexo, cada uno codificado en dos niveles, solo hay cuatro patrones posibles de factor/covariable. Si usted ingresa los datos como frecuencias o como éxitos, ensayos o fracasos, cada fila contiene un patrón de factor/covariable.
Probabilidad del evento
Las probabilidades del evento son πk para k = 1, 2, ..., K.
Fórmula
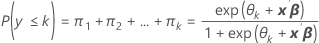
Notación
| Término | Description |
|---|---|
| k | es igual a 1, ..., K – 1 |
| θk | constante |
| β | vector de coeficientes de la ecuación logit |
Probabilidad acumulada del evento
La probabilidad de que la respuesta esté en la categoría k o una categoría inferior, para cada k posible. La késima probabilidad acumulada es:
Fórmula
P(y k) = p1 + ... + pk,k = 1, ... , K
k) = p1 + ... + pk,k = 1, ... , K
Las probabilidades acumuladas reflejan el orden de la respuesta. Para un modelo con k categorías de respuesta:
P(y 1) <P(y
1) <P(y 2)
2)  …
… P(y
P(y K) = 1
K) = 1

Coeficiente
Minitab utiliza el modelo de probabilidades proporcionales donde un vector de predictores, x, tiene un parámetro β que describe el efecto de x sobre las probabilidades logarítmicas de la respuesta en la categoría k o inferior. Minitab presupone un efecto idéntico de x para todas las categorías K – 1, por lo que solo se calcula 1 coeficiente para cada predictor. El coeficiente del predictor indica que para cualquier k fija, el cambio estimado en el logit de la respuesta cuando el predictor está en un nivel en comparación con el nivel de referencia.
Minitab estima una constante para cada K – 1 categoría. Utilice las estimaciones de parámetros para calcular las probabilidades estimadas para cada categoría usando el modelo de las probabilidades acumuladas:
Fórmula
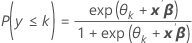
Los coeficientes estimados se calculan usando un método iterativo reponderado de mínimos cuadrados, que es equivalente a la estimación de máxima verosimilitud.1,2
Referencias
- D.W. Hosmer y S. Lemeshow (2000). Applied Logistic Regression. 2nd ed. John Wiley & Sons, Inc.
- P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Error estándar de los coeficientes
El error estándar asintótico, que indica la precisión del coeficiente estimado. Cuanto menor sea el error estándar, más precisa será la estimación.
Para obtener más información, véase [1] y [2].
- A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
- P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
Z se utiliza para determinar si el predictor está significativamente relacionado con la respuesta. Valores absolutos más grandes de Z indican una relación significativa. El valor p indica donde se encuentra Z en la distribución normal.
Fórmula
Z = βi / error estándar
La fórmula para la constante es:
Z = θk / error estándar
Para muestras pequeñas, la prueba de relación de probabilidades puede ser una prueba de significancia más fiable.
Valor p (P)
Se utilizan en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula. El valor p es la probabilidad de obtener un estadístico de prueba que sea por lo menos tan extremo como el valor real calculado, si la hipótesis nula es verdadera. Un valor de corte que se utiliza comúnmente para el valor p es 0.05. Por ejemplo, si el valor p calculado de un estadístico de prueba es menor que 0.05, usted rechaza la hipótesis nula.
Relación de probabilidades
Minitab utiliza un modelo de probabilidades proporcionales para la regresión logística ordinal. Solo se calcula un parámetro y una relación de probabilidades para cada predictor. La relación de probabilidades utiliza las probabilidades acumuladas y sus complementos. Para un predictor con 2 niveles x1 y x2, la relación de probabilidades acumulada es:
Fórmula
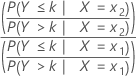
Intervalo de confianza
Fórmula
El intervalo de confianza de muestras grandes para βi es:
β i + Zα /2* (error estándar)
Para obtener el intervalo de confianza de la relación de probabilidades, eleve a una potencia los límites inferior y superior del intervalo de confianza. El intervalo proporciona el rango en el que podrían situarse las probabilidades para cada cambio de una unidad en el predictor.
Notación
| Término | Description |
|---|---|
| α | nivel de significancia |
Log-verosimilitud
Derivada de las funciones de densidad de las probabilidades individuales, la expresión se maximiza para producir valores óptimos de β. La log-verosimilitud no puede utilizarse por sí sola como una medida de ajuste, porque depende del tamaño de la muestra, pero se puede usar para comparar dos modelos.
Para la regresión logística ordinal, existen n vectores multinomiales independientes, cada uno con k categorías. Estas observaciones se denotan con y1, ..., yn, donde yi = (yi1, ..., yik) y Σjyij = mi es fijo para cada i. De la iésima observación yi, la contribución a la log-verosimilitud es:
Fórmula
L(πi ; yi) = Σkyik log πik
La log-verosimilitud total es una suma de las contribuciones de cada una de las n observaciones:
L(π ; y) = Σi L(πi; yi)
Notación
| Término | Description |
|---|---|
| πik | probabilidad de la iésima observación para la késima categoría |
Matriz de varianzas-covarianzas
Una matriz cuadrada con las dimensiones p + K – 1. La varianza de cada coeficiente se encuentra en la celda diagonal y la covarianza de cada par de coeficientes se encuentra en la celda adecuada adyacente a la diagonal. La varianza es el error estándar del coeficiente elevado al cuadrado.
La matriz de varianzas-covarianzas es asintótica y se obtiene a partir de la última iteración de la inversa de la matriz de información.
Notación
| Término | Description |
|---|---|
| p | número de predictores |
| K | número de categorías en la respuesta |
Pearson
Un estadístico de resumen basado en los residuos de Pearson que indica qué tan bien se ajusta el modelo a los datos. Pearson no es útil cuando el número de valores distintos de la covariable es aproximadamente igual al número de observaciones, pero sí es útil cuando se tienen observaciones repetidas en el mismo nivel de la covariable. Estadísticos de prueba X2 más altos y valores p más bajos indican que el modelo podría no ajustarse adecuadamente a los datos.
La fórmula es:
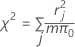
donde r = residuo de Pearson, m = número de ensayos en el jésimo patrón de factor/covariable y π0 = valor hipotético para la proporción.
Desviación
Un estadístico de resumen basado en los residuos de desviación que indica qué tan bien se ajusta el modelo a los datos. La desviación no es útil cuando el número de valores distintos de la covariable es aproximadamente igual al número de observaciones, pero sí es útil cuando se tienen observaciones repetidas en el mismo nivel de la covariable. Valores más altos de D y valores p más bajos indican que el modelo podría no ajustarse adecuadamente a los datos. Los grados de libertad para la prueba son (k - 1)* J − (p) donde k es el número de categorías en la respuesta, J es el número de patrones distintos de factor-covariable y p es el número de coeficientes.
La fórmula es:
D =2 Σ yik log p ik− 2 Σ yik log π ik
donde πik = probabilidad de la iésima observación para la késima categoría.
Medidas de asociación
Los pares concordantes y discordantes indican qué tan bien el modelo predice los datos. Mientras más pares concordantes tenga usted, mejor será la capacidad predictiva del modelo.
La tabla de pares concordantes, discordantes y de valores iguales se calcula formando todos los pares posibles de observaciones con valores de respuesta diferentes. Supongamos que los valores de respuesta son 1, 2 y 3. Minitab parea cada observación con el valor de respuesta 1 con cada observación con los valores de respuesta 2 y 3 y luego parea cada observación con el valor de respuesta 2 con cada observación con los valores de respuesta 1 y 3. El número total de pares es igual al número de observaciones con la respuesta 1 multiplicado por el número de observaciones con la respuesta 2 más el número de observaciones con la respuesta 1 multiplicado por el número de observaciones con la respuesta 3 más el número de observaciones con la respuesta 2 multiplicado por el número de observaciones con la respuesta 3.
Para determinar si los pares son concordantes o discordantes, Minitab calcula las probabilidades pronosticadas acumuladas de cada observación y compara estos valores para cada par de observaciones.
- Concordante
- Para los pares que incluyen el valor de respuesta más bajo (que en el ejemplo anterior es 1), un par es concordante si la probabilidad acumulada hasta el valor de respuesta más bajo es mayor para la observación con el valor de respuesta más bajo que para la observación con el valor de respuesta más alto. Para los pares con los valores de respuesta más altos (en el ejemplo anterior, los pares con 2 y 3), un par es concordante si la probabilidad acumulada hasta 2 es mayor para la observación con el valor de respuesta 2 que para la observación con el valor de respuesta 3.
- Discordante
- Para los pares que incluyen el valor de respuesta más bajo (que en el ejemplo anterior es 1), un par es discordante si la probabilidad acumulada hasta el valor de respuesta más bajo es mayor para la observación con el valor de respuesta más alto que para la observación con el valor de respuesta más bajo. Para los pares con los valores de respuesta más altos (en el ejemplo anterior, los pares con 2 y 3), un par es discordante si la probabilidad acumulada hasta 2 es mayor para la observación con el valor de respuesta 3 que para la observación con el valor de respuesta 2.
- Empates
- Un par tiene valores iguales si las observaciones tienen probabilidades acumuladas iguales.
Fórmula
Usando la tabla de pares concordantes, discordantes y de valores iguales, Minitab calcula las siguientes medidas de resumen:



Notación
| Término | Description |
|---|---|
| nc | número de pares concordantes |
| nd | número de pares discordantes |
| nt | número de pares con valores iguales |
| N | número total de observaciones |
