Seleccione el método o la fórmula de su preferencia.
En este tema
Restricciones de parámetros
Para aplicar las restricciones de parámetros, transforme los parámetros.1
| Si | Entonces |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| Término | Description |
|---|---|
| a y b | constantes numéricas |
| θ | parámetros |
| φ | parámetros transformados |
Minitab realiza estas transformaciones y muestra los resultados en términos de los parámetros originales.
- Bates y Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
Error estándar de la estimación de parámetro
El error estándar aproximado de la estimación de θp es S veces la raíz cuadrada del elemento diagonal p de 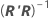 , que se escribe como:
, que se escribe como:

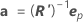

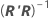 , que se escribe como:
, que se escribe como:

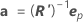

Notación
| Término | Description |
|---|---|
| n | nésima observación |
| N | número total de observaciones |
| p | número de parámetros libres (no bloqueados) |
| R | la matriz R (triangular superior) de la descomposición QR de Vi para la iteración final |
| v0 | matriz de gradientes = ( ∂f(xn, θ) / ∂θp), el vector P por 1 de las derivadas parciales de f(x0, θ), evaluadas en θ* |
| S |
 |
Matriz de correlación de las estimaciones de parámetros
La matriz aproximada de varianzas-covarianzas de las estimaciones de parámetros es:
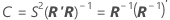
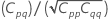

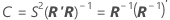
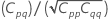

Notación
| Término | Description |
|---|---|
| R | la matriz R (triangular superior) de la descomposición QR de Vi para la iteración final |
| P | número de parámetros libres (no bloqueados) |
| v0 | matriz de gradientes = ( ∂f(xn, θ) / ∂θp), el vector P por 1 de las derivadas parciales de f(x0, θ), evaluadas en θ* |
| θ | parámetros |
Intervalos de confianza de la verosimilitud del perfil para los parámetros
Sea θ = (θ1, . . . . θp) * con θ* la iteración final para θ.
Los límites de confianza de 100 (1 - α) % basados en la verosimilitud satisfacen:
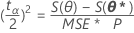
donde S( θp ) es la SSE obtenida al mantener θp fijo y minimizar los otros parémetros.1 Esto es equivalente a resolver:
S(θp) = S(θ*) + (tα/2)2 MSE
Notación
| Término | Description |
|---|---|
| θ | parámetros |
| n | nésima observación |
| N | número total de observaciones |
| P | número de parámetros libres (no bloqueados) |
| tα/2 | punto superior α/2 de la distribución t con N - P grados de libertad |
| S(θ) | Suma de los cuadrados del error |
| MSE | cuadrado medio del error |
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
