Métodos en Regresión no lineal

La función de expectativa para la observación n se denota mediante:

Minitab considera la función de expectativa de todas las observaciones N como una función de los parámetros con valores de vector, como:

que es un vector N X 1 con los elementos .

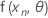
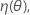
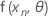La jacobiana de η es una matriz N X P con elementos que son iguales a las derivadas parciales de la función de expectativa con respecto a los parámetros:

Sea Vⁱ = V(θⁱ) la jacobiana evaluada en θⁱ, la estimación del parámetro después de la iteración i.

Entonces una aproximación lineal para η es:

que constituye la base del método de Gauss-Newton y para las inferencias aproximadas.

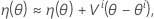
θ* denota la estimación de mínimos cuadrados.

Por opción predeterminada, Minitab utiliza el método de Gauss-Newton para determinar la estimación de mínimos cuadrados. El método utiliza una aproximación lineal a la función de expectativa para mejorar iterativamente una conjetura inicial θ⁰ para θ, y luego el método sigue mejorando las estimaciones hasta que el desplazamiento relativo esté por debajo de la tolerancia¹ prescrita. Es decir, Minitab expande la función de expectativa f(x_n,θ) en una serie de Taylor de primer orden alrededor de θ⁰ como:

donde

con p = 1, 2,..., p

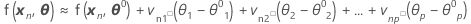
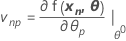
Incluyendo todos los casos N

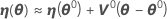
donde V⁰ es la matriz de derivadas NxP con los elementos {v_np}. Esto es equivalente a hacer una aproximación de los residuos, z(θ) = y - η(θ), mediante:

donde

y

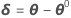
Minitab calcula el incremento de Gauss δ⁰para minimizar la suma de los cuadrados de los residuos aproximados 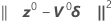, usando:

y entonces: .

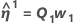
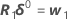El punto

ahora debe estar más cerca de y que η(θ⁰) y Minitab utiliza el valor θ¹ = θ⁰ + δ⁰ para realizar otra iteración calculando nuevos residuos z¹ = y - η(θ¹), una nueva matriz de derivadas V¹ y un nuevo incremento. Minitab repite este proceso hasta la convergencia, que es cuando el incremento es tan pequeño que no hay ningún cambio útil en los elementos del vector de parámetros.

A veces el incremento de Gauss-Newton produce un aumento en la suma de los cuadrados. Cuando esto ocurre, la aproximación lineal aún es una aproximación cercana a la superficie real para una región lo suficientemente pequeña alrededor de η(θ⁰). Para reducir la suma de los cuadrados, Minitab incorpora un factor de paso λ y calcula:

Minitab comienza con λ = 1 y lo divide por la mitad hasta que S(θ¹) < S( θ⁰).

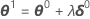
1. Bates y Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Cuando las columnas de la matriz de gradientes V tienen colinealidad, esta puede volverse singular, causando un comportamiento errático de las iteraciones de Gauss-Newton. Para resolver la singularidad, Minitab puede modificar el incremento de Gauss-Newton al compromiso de Levenberg:

o el compromiso de Marquardt:

donde k es un factor condicionante y D una matriz diagonal con entradas que son iguales a los elementos diagonales de V^TV. La dirección de δ(k) es intermedia entre la dirección del incremento de Gauss-Newton (k → 0) y la dirección del descenso más pronunciado:

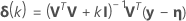
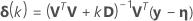
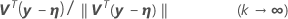.¹

1. Bates y Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Por opción predeterminada, Minitab declara convergencia cuando el desplazamiento relativo es menor que 1.0e-5. Esto asegura que las inferencias no se vean afectadas significativamente por el hecho de que el vector actual de parámetros sea menos de 0.001% del radio del disco de la región de confianza desde el punto de mínimos cuadrados.¹

1. Bates y Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.