En este tema
Paso 1: Determinar si la línea de regresión se ajusta a los datos
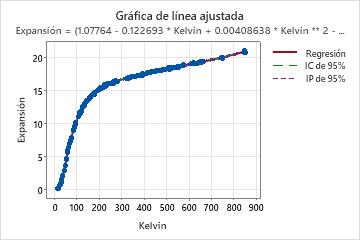
Si el modelo no lineal contiene un predictor, Minitab muestra la gráfica de línea ajustada para mostrar la relación entre la respuesta y los datos predictores. La gráfica incluye la línea de regresión, que representa la ecuación de regresión. Usted también puede elegir mostrar los intervalos de confianza y de predicción de 95% en la gráfica.
- La muestra contiene un número adecuado de observaciones a lo largo del rango completo de todos los valores predictores.
- El modelo se ajusta adecuadamente a la curvatura en los datos. Para determinar cual modelo es mejor, examine la gráfica, el error estándar de la regresión (S), y la prueba de falta de ajuste cuando los datos contienen réplicas.
- Busque cualquier valor atípico, que pueda tener un efecto fuerte sobre los resultados. Intente identificar la causa de cualesquiera valores atípicos. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). Luego, repita el análisis. Para obtener más información sobre cómo detectar valores atípicos, vaya a Observaciones poco comunes.
Paso 2: Examinar la relación entre los predictores y la respuesta
Utilice la ecuación de regresión para describir la relación entre la respuesta y los términos incluidos en el modelo. La ecuación de regresión es una representación algebraica de la línea de regresión. Ingrese el valor de cada predictor en la ecuación para calcular el valor de respuesta medio. A diferencia de la regresión lineal, una ecuación de regresión no lineal puede tomar muchas formas diferentes.
En el caso de las ecuaciones no lineales, determinar el efecto que tiene cada predictor sobre la respuesta puede ser menos intuitivo que para las ecuaciones lineales. A diferencia de las estimaciones del parámetro, no hay una interpretación consistente para las estimaciones del parámetro en los modelos no lineales. La correcta interpretación para cada parámetro depende de la función de expectativa y la posición del parámetro en ella. Si el modelo no lineal contiene solamente un predictor, evalúe la gráfica de línea ajustada para observar la relación entre el predictor y la respuesta.
Si necesita determinar si una estimación de parámetro es estadísticamente significativa, utilice los intervalos de confianza para los parámetros. El parámetro es estadísticamente significativo si el rango excluye el valor de la hipótesis nula. Minitab no puede calcular valores p para parámetros en una regresión no lineal. En el caso de la regresión lineal, el valor de la hipótesis nula para cada parámetro es 0, para que no haya efecto, y el valor p se basa en este valor. Sin embargo, en la regresión no lineal, el valor correcto de la hipótesis nula para cada parámetro depende de la función de expectativa y la posición del parámetro en ella.
Para algunos conjuntos de datos, funciones de expectativa y niveles de confianza, es posible que no exista uno o ambos límites de confianza. Minitab indica los resultados faltantes con un asterisco. Si el intervalo de confianza tiene un límite faltante, un nivel de confianza más bajo podría producir un intervalo bilateral.
La convergencia en una solución no necesariamente garantiza que el ajuste del modelo sea óptimo o que la suma de cuadrados de error (SSE) sea minimizada. La convergencia en valores de parámetros incorrectos puede ocurrir debido a una SSE local mínima o a una función de expectativa incorrecta. Por lo tanto, es crucial examinar los valores de parámetros, la gráfica de línea ajustada y las gráficas de residuos, para determinar si el ajuste del modelo y los valores de parámetros son razonables.
Ecuación
3) / (1 - 0.00576099 * Kelvin + 0.000240537 * Kelvin ** 2 - 1.23144E-07 * Kelvin ** 3)
Resultado clave: Ecuación
En estos resultados, hay un predictor y siete estimaciones del parámetro. La variable de respuesta es Expansión y la variable predictora es temperatura en la escala de Kelvin. La larga ecuación describe la relación entre la respuesta y los predictores. El efecto que un incremento de 1 grado Kelvin tiene sobre la expansión del cobre depende en gran medida de la temperatura inicial. El efecto de los cambios de temperatura sobre la expansión del cobre no se puede resumir fácilmente. Evalúe la gráfica de línea ajustada para observar la relación entre el predictor y una respuesta.
Si ingresa un valor para la temperatura en Kelvin a la ecuación, el resultado es el valor ajustado para la expansión del cobre.
Paso 3: Determinar qué tan bien se ajusta el modelo a los datos
Para determinar qué tan bien se ajusta el modelo a los datos, examine los estadísticos de la tabla Resumen del modelo y la tabla Falta de ajuste.
- S
-
Utilice S para evaluar qué tan bien el modelo describe la respuesta.
S se mide en las unidades de la variable de respuesta y representa la distancia que separa a los valores de los datos de los valores ajustados. Mientras más bajo sea el valor de S, mejor describirá el modelo la respuesta. Sin embargo, un valor de S bajo no indica por sí solo que el modelo cumple con los supuestos del modelo. Debe examinar las gráficas de residuos para verificar los supuestos.
- Falta de ajuste
-
Minitab muestra automáticamente la tabla Falta de ajuste cuando los datos contienen réplicas. Las réplicas son múltiples observaciones con valores predictores idénticos. Si los datos no contienen réplicas, es imposible calcular el error puro que se necesita para realizar esta prueba. Los diferentes valores de respuesta de las réplicas representan el error puro, porque solo la variación aleatoria puede provocar diferencias entre los valores de respuesta observados.
Para determinar si el modelo especifica correctamente la relación entre la respuesta y los predictores, compare el valor p de la prueba de falta de ajuste con el nivel de significancia para evaluar la hipótesis nula. La hipótesis nula para la prueba de falta de ajuste es que el modelo especifica correctamente la relación entre la respuesta y los predictores. Por lo general, un nivel de significancia (denotado como alfa o α) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que el modelo no especifica correctamente la relación entre la respuesta y los predictores cuando el modelo sí especifica la relación correcta.- Valor p ≤ α: La falta de ajuste es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted concluye que el modelo no especifica correctamente la relación. Para mejorar el modelo, es posible que tenga que agregar términos o transformar los datos.
- Valor p > α: La falta de ajuste no es estadísticamente significativa
-
Si el valor p es mayor que el nivel de significancia, la prueba no detecta ninguna falta de ajuste.
Falta de ajuste
| Fuente | GL | SC | MC | F | P |
|---|---|---|---|---|---|
| Error | 229 | 1.53244 | 0.0066919 | ||
| Falta de ajuste | 228 | 1.52583 | 0.0066922 | 1.01 | 0.679 |
| Error puro | 1 | 0.00661 | 0.0066125 |
Resumen
| Iteraciones | 15 |
|---|---|
| SSE final | 1.53244 |
| DFE | 229 |
| MSE | 0.0066919 |
| S | 0.0818039 |
Resultados clave: S, falta de ajuste
En estos resultados, S indica que la desviación estándar de la distancia entre los valores de datos y los valores ajustados es aproximadamente 0.08 unidades. El valor p para la prueba de falta de ajuste es 0.679, que no proporciona ninguna evidencia de que el ajuste del modelo a los datos sea deficiente.
Paso 4: Determinar si el modelo cumple con los supuestos del análisis
Utilice las gráficas de residuos como ayuda para determinar si el modelo es adecuado y cumple con los supuestos del análisis. Si los supuestos no se cumplen, el modelo podría no ajustarse adecuadamente a los datos y se debería tener cuidado al interpretar los resultados.
Para obtener más información sobre cómo manejar los patrones en las gráficas de residuos, vaya a Gráficas de residuos para Regresión no lineal y haga clic en el nombre de la gráfica de residuos en la lista que se encuentra en la parte superior de la página.
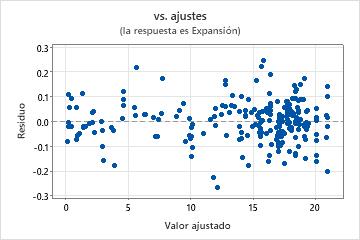
Gráfica de residuos vs. ajustes
Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
| Un punto que está lejos de los otros puntos en la dirección x | Un punto influyente |
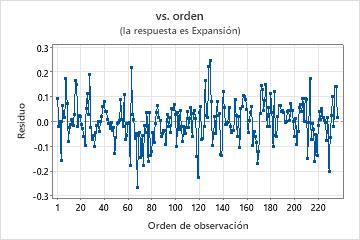
Gráfica de residuos vs. orden
Tendencia
Cambio
Ciclo
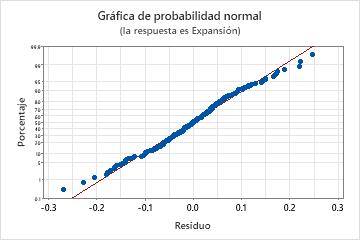
Gráfica de probabilidad normal de los residuos
Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| No una línea recta | No normalidad |
| Un punto que está alejado de la línea | Un valor atípico |
| Pendiente cambiante | Una variable no identificada |