Gráfica de línea ajustada
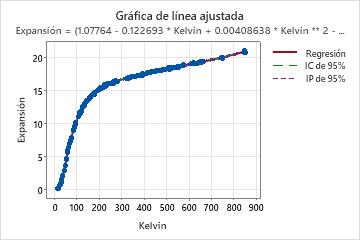
Si el modelo no lineal contiene un predictor, Minitab muestra la gráfica de línea ajustada para mostrar la relación entre la respuesta y los datos predictores. La gráfica incluye la línea de regresión, que representa la ecuación de regresión. Usted también puede elegir mostrar los intervalos de confianza y de predicción de 95% en la gráfica.
Interpretación
- La muestra contiene un número adecuado de observaciones a lo largo del rango completo de todos los valores predictores.
- El modelo se ajusta adecuadamente a la curvatura en los datos. Para determinar cual modelo es mejor, examine la gráfica, el error estándar de la regresión (S), y la prueba de falta de ajuste cuando los datos contienen réplicas.
- Busque cualquier valor atípico, que pueda tener un efecto fuerte sobre los resultados. Intente identificar la causa de cualesquiera valores atípicos. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). Luego, repita el análisis. Para obtener más información sobre cómo detectar valores atípicos, vaya a Observaciones poco comunes.
Ecuación
Utilice la ecuación de regresión para describir la relación entre la respuesta y los términos en el modelo. La ecuación de regresión es una representación algebraica de la línea de regresión. Ingrese el valor de cada predictor en la ecuación para calcular el valor de respuesta medio. A diferencia de la regresión lineal, una ecuación de regresión no lineal puede tomar muchas formas diferentes.
En el caso de las ecuaciones no lineales, determinar el efecto que tiene cada predictor sobre la respuesta puede ser menos intuitivo que para las ecuaciones lineales. A diferencia de las estimaciones del parámetro, no hay una interpretación consistente para las estimaciones del parámetro en los modelos no lineales. La correcta interpretación para cada parámetro depende de la función de expectativa y la posición del parámetro en ella. Si el modelo no lineal contiene solamente un predictor, evalúe la gráfica de línea ajustada para observar la relación entre el predictor y la respuesta.
La convergencia en una solución no necesariamente garantiza que el ajuste del modelo sea óptimo o que la suma de cuadrados de error (SSE) sea minimizada. La convergencia en valores de parámetros incorrectos puede ocurrir debido a una SSE local mínima o a una función de expectativa incorrecta. Por lo tanto, es crucial examinar los valores de parámetros, la gráfica de línea ajustada y las gráficas de residuos, para determinar si el ajuste del modelo y los valores de parámetros son razonables.
Interpretación
En estos resultados, hay un predictor y siete estimaciones del parámetro. La variable de respuesta es Expansión y la variable predictora es temperatura en la escala de Kelvin. La larga ecuación describe la relación entre la respuesta y los predictores. El efecto que un incremento de 1 grado Kelvin tiene sobre la expansión del cobre depende en gran medida de la temperatura inicial. El efecto de los cambios de temperatura sobre la expansión del cobre no se puede resumir fácilmente. Evalúe la gráfica de línea ajustada para observar la relación entre el predictor y una respuesta.
Si ingresa un valor para la temperatura en Kelvin a la ecuación, el resultado es el valor ajustado para la expansión del cobre.
Ecuación
3) / (1 - 0.00576099 * Kelvin + 0.000240537 * Kelvin ** 2 - 1.23144E-07 * Kelvin ** 3)
IC de 95%
El intervalo de confianza para el ajuste proporciona un rango de valores probables para la respuesta media dada la configuración especificada de los predictores.
Interpretación
Utilice el intervalo de confianza para evaluar la estimación del valor ajustado para los valores observados de las variables.
Por ejemplo, con un nivel de confianza de 95%, usted puede estar 95% seguro de que el intervalo de confianza contiene la media de la población para los valores especificados de las variables incluidas en el modelo. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Un intervalo de confianza amplio indica que usted puede estar menos seguro acerca de la media de los valores futuros. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
IP de 95%
El intervalo de predicción es un rango que es probable que contenga una respuesta futura individual para un valor de la variable predictora, dada la configuración especificada de los predictores.
Interpretación
Por ejemplo, un ingeniero de materiales que trabaja en una fábrica de muebles desarrolla un modelo de regresión simple para predecir la rigidez del tablero de partículas a partir de la densidad del tablero. El ingeniero verifica que el modelo cumple con los supuestos del análisis. Luego, el analista utiliza el modelo para predecir la rigidez.
La ecuación de regresión predice que la rigidez de una nueva observación será 66.995 y el intervalo de predicción es [50, 85]. Aunque es poco probable que dicha observación tenga exactamente una rigidez de 66.995, el intervalo de predicción indica que el ingeniero puede estar 95% seguro de que el valor real estará aproximadamente entre 50 y 85.
El intervalo de predicción siempre es más amplio que el intervalo de confianza correspondiente debido a la incertidumbre adicional que implica la predicción de una respuesta individual en comparación con la media de múltiples respuestas.
