En este tema
Modelos de regresión polinomial
Fórmula
Usted puede ajustar los siguientes modelos de regresión lineales, cuadráticos o cúbicos:
| Tipo de modelo | Orden | Modelo estadístico |
|---|---|---|
| lineal | primero | Y = β0+ β1x + e |
| cuadrático | segundo | Y = β0+ β1x + β2x2+ e |
| cúbico | tercero | Y = β0+ β1x + β2x2+ β3x3+ e |
Otra forma de modelar la curvatura es generar modelos adicionales utilizando el logaritmo base 10 de X y/o Y para los modelos lineales, cuadráticos y cúbicos. Además, el sacar el logaritmo base 10 de Y puede servir para reducir la asimetría hacia la derecha o la varianza no constante de los residuos.
Cuando Minitab ajusta los modelos cuadráticos o cúbicos, estandariza los predictores antes de estimar los coeficientes. La estandarización reduce la multicolinealidad entre los predictores. La reducción asegura que la multicolinealidad sea tan baja que Minitab no pueda excluir ningún predictor del modelo. La salida muestra los coeficientes estandarizados en las unidades originales de los predictores.
Coeficiente (Coef)
La fórmula para el coeficiente o la pendiente en regresión lineal simple es:
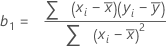
La fórmula para la intersección (b0) es:

En términos de matrix, la fórmula que calcula el vector de coeficientes en la regresión múltiple es:
b = (X'X)-1X'y
Notación
| Término | Description |
|---|---|
| yi | valor de la iésima respuesta observada |
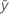 | respuesta media |
| xi | iésimo valor predictor |
 | predictor medio |
| X | matriz de diseño |
| y | matriz de respuesta |
S

Notación
| Término | Description |
|---|---|
| MSE | cuadrado medio del error |
R-cuad.


R2 también se puede calcular como la correlación cuadrada de y y 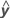 .
.
Notación
| Término | Description |
|---|---|
| SC | Suma de los cuadrados |
| y | variable de respuesta |
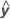 | variable de respuesta ajustada |
R-cuad.(ajustado)

Notación
| Término | Description |
|---|---|
| CM | Cuadrado medio |
| SC | Suma de los cuadrados |
| GL | Grados de libertad |
Grados de libertad (GL)
Los grados de libertad para cada componente del modelo son:
| Fuentes de variación | GL |
|---|---|
| Regresión | p |
| Error | n – p – 1 |
| Total | n – 1 |
- Los datos contienen múltiples observaciones con los mismos valores predictores.
- Los datos contienen los puntos correctos para estimar términos adicionales que no están en el modelo.
Notación
| Término | Description |
|---|---|
| n | número de observaciones |
| p | número de coeficientes en el modelo, sin contar la constante |
SC Ajust.
La suma de las distancias elevadas al cuadrado. La SC de regresión es la porción de la variación explicada por el modelo. La SC del error es la porción no explicada por el modelo y se atribuye al error. La SC total es la variación total en los datos.
Fórmula

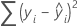
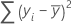
Notación
| Término | Description |
|---|---|
| yi | valor de la iésima respuesta observada |
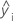 | iésima respuesta ajustada |
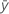 | respuesta media |
CM ajustado – Error
El cuadrado medio del error (también abreviado como CM error o MSE y conocido como s2) es la varianza alrededor de la línea de regresión ajustada. La fórmula es:
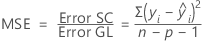
Notación
| Término | Description |
|---|---|
| yi | iésimo valor de respuesta observado |
 | iésima respuesta ajustada |
| n | número de observaciones |
| p | número de coeficientes en el modelo, sin contar la constante |
CM ajust – Regresión
La fórmula del cuadrado medio (CM) de la regresión es:
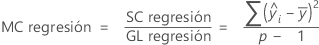
Notación
| Término | Description |
|---|---|
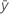 | respuesta media |
 | iésima respuesta ajustada |
| p | número de términos en el modelo |
CM Ajust. – Total
La fórmula para el cuadrado medio (CM) total es:
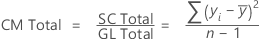
Notación
| Término | Description |
|---|---|
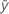 | respuesta media |
| yi | valor de la iésima respuesta observada |
| n | número de observaciones |
Valor F
Las fórmulas para el estadístico F son las siguientes:
- F(Regresión)
-
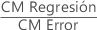
- F(Término)
-

- F(Falta de ajuste)
-

Notación
| Término | Description |
|---|---|
| CM Regresión | Una medida de la variación en la respuesta que explica el modelo actual. |
| CM Error | Una medida de la variación que el modelo no explica. |
| CM Término | Una medida de la cantidad de variación que un término explica después de justificar los otros términos incluidos en el modelo. |
| CM Falta de ajuste | Una medida de la variación en la respuesta que podría modelarse al agregar más términos al modelo. |
| CM Error puro | Una medida de la variación en los datos de respuesta replicados. |
Valor p – Tabla Análisis de varianza
El valor p es una probabilidad que se calcula a partir de una distribución F con los grados de libertad (GL) que se indican a continuación:
- GL del numerador
- suma de los grados de libertad para el término o los términos en la prueba
- GL del denominador
- grados de libertad para el error
Fórmula
1 − P(F ≤ fj)
Notación
| Término | Description |
|---|---|
| P(F ≤ f) | función de distribución acumulada para la distribución F |
| f | estadístico F para la prueba |
Residuo (Resid.)
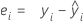
Notación
| Término | Description |
|---|---|
| ei | i ésimo residuo |
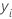 | i ésimo valor de respuesta observado |
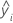 | i iésima respuesta ajustada |
