En este tema
Regresión ponderada
La regresión de mínimos cuadrados ponderados es un método para tratar las observaciones que tienen varianzas no constantes. Si las varianzas no son constantes, a las observaciones con:
- a las grandes varianzas se les debe ofrecer ponderaciones relativamente pequeñas
- a las pequeñas varianzas se les debe ofrecer ponderaciones relativamente grandes
La elección de ponderaciones generalmente es la inversa de la varianza de error puro en la respuesta.
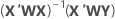
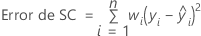
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
| W | una matriz n x n con las ponderaciones en la diagonal |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| wi | ponderación de la iésima observación |
| yi | valor de respuesta de la iésima observación |
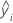 | valor ajustado de la iésima observación |
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 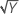 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Ecuación de regresión
Para un modelo con múltiples predictores, la ecuación es:
y = β0 + β1x1 + ... + βkxk + ε
La ecuación ajustada es:
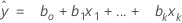
En la regresión lineal simple, que incluye solo un predictor, el modelo es:
y=ß0+ ß1x1+ε
Usando estimaciones de regresión b0 para ß0y b1 para ß1, la ecuación ajustada es:
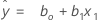
Ecuaciones con una variable categórica
- Ecuación separada de cada conjunto de niveles predictores categóricos
- Una sola ecuación
- C1
- La variable respuesta
- C2
- Un predictor continuo
- C3
- Una variable predictora categórica con los niveles Rojo y Azul
- Azul: C1 = 0,184 + 0,1964*C2
- Rojo: C1 = 0,011 + 0,1964*C2
Una sola ecuación utiliza una variable indicadora para representar la variable categórica.
C1 = 0,184 + 0,1964*C2 + 0,0*C3_Azul- 0,173*C3_Rojo
- Observación azul (C3_Azul = 1, C3_Rojo = 0): C1 = 0,184 + 0,1964*C2 + 0,0*1 - 0,173*0 = 0,184 + 0,1964*C2
- Observación roja (C3_Azul = 0, C3_Rojo = 1: C1 = 0,084 + 0,1964*C2 + 0,0*0 - 0,173*1 = 0,011 + 0,1964*C2
Notación
| Término | Description |
|---|---|
| y | Respuesta |
| xk | Ok-ésimo trimestre. Cada término puede ser un solo predictor, un término polinómico o un término de interacción. |
| ßk | késimo coeficiente de regresión poblacional |
| ε | término de error que sigue una distribución normal con una media de 0 |
| bk | Estimación del coeficiente de regresión poblacional késimo |
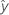 | respuesta ajustada |
Matriz de diseño
La matriz de diseño contiene los predictores en una matriz (X) con n filas, donde n es el número de observaciones. Hay una columna para cada coeficiente del modelo.
Los predictores categóricos se codifican utilizando la codificación 1, 0 ó -1, 0, 1. X no incluye una columna para el nivel de referencia del factor.
Para calcular las columnas de un término de interacción, multiplique todos los valores correspondientes de los predictores incluidos en la interacción. Por ejemplo, supongamos que la primera observación tiene un valor de 4 para el predictor A y un valor de 2 para el predictor B. En la matriz de diseño, la interacción entre A y B se representa como 8 (4 x 2).
Inversa de x'x
Cómo elimina Minitab los predictores muy correlacionados de la ecuación de regresión en Ajustar modelo de regresión
Sea rij el elemento de la matriz con barrido actual asociada con Xi y Xj.
Las variables se ingresan o se eliminan una a la vez. Xk es elegible para ingreso si es una variable independiente que no se encuentra actualmente en el modelo con rkk ≥ 1 (tolerancia con un valor predeterminado de 0.0001) y también para cada variable Xj que se encuentra actualmente en el modelo,
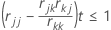
- Minitab aplica el método SWEEP (barrido) a la matriz de correlación, R, tratando a X1 … Xp como si fueran variables aleatorias.
- Para cualquier predictor continuo, Minitab compara el elemento rkk con la tolerancia; rkk ≥ tolerancia, donde k = 1 hasta p.
- Para cada variable Xj actualmente en el modelo, Minitab verifica que (rjj – rjk * (rkj / rkk)) * tolerancia ≤ 1.
Nota
Donde rkk, rjk, rjj son los elementos diagonales y fuera de la diagonal correspondientes para la variable Xj y Xk después de las operaciones SWEEP del paso k.
- De lo contrario, el predictor no pasa la prueba y es eliminado del modelo.
Nota
El valor de tolerancia predeterminado es 8.8e–12.
Nota
Usted puede usar el subcomando TOLERANCE con el comando de sesión REGRESS para hacer que Minitab mantenga en el modelo un predictor que esté muy correlacionado con otro predictor. Sin embargo, bajar la tolerancia podría ser peligroso debido a la posibilidad de que se produzcan resultados numéricamente inexactos.
