Seleccione el método o la fórmula de su preferencia.
En este tema
Coeficiente (Coef)
La fórmula para el coeficiente o la pendiente en regresión lineal simple es:
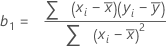
La fórmula para la intersección (b0) es:

En términos de matrix, la fórmula que calcula el vector de coeficientes en la regresión múltiple es:
b = (X'X)-1X'y
Notación
| Término | Description |
|---|---|
| yi | valor de la iésima respuesta observada |
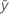 | respuesta media |
| xi | iésimo valor predictor |
 | predictor medio |
| X | matriz de diseño |
| y | matriz de respuesta |
Error estándar del coeficiente (EE Coef)
Para la regresión lineal simple, el error estándar del coeficiente es:
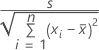
Los errores estándar de los coeficientes para la regresión múltiple son las raíces cuadradas de los elementos diagonales de esta matriz:
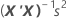
Notación
| Término | Description |
|---|---|
| xi | iésimo valor predictor |
 | media del predictor |
| X | matriz de diseño |
| X' | transposición de la matriz de diseño |
| s2 | cuadrado medio del error |
Valor t
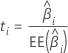
Notación
| Término | Description |
|---|---|
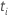 | estadístico de prueba para el  coeficiente coeficiente |
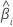 |  coeficiente estimado coeficiente estimado |
 | error estándar del  coeficiente estimado coeficiente estimado |
Valor p – Tabla Coeficientes
El valor p bilateral para la hipótesis nula de que un coeficiente de regresión equivale a 0 es:
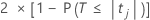
Los grados de libertad son los grados de libertad para el error, de la manera siguiente:
n – p – 1
Notación
| Término | Description |
|---|---|
 | La función de distribución acumulativa de la distribución t con grados de libertad equivale a los grados de libertad de error. |
| tj | El estadístico t para el jésimo coeficiente. |
| n | El número de observaciones en el conjunto de datos. |
| p | La suma de los grados de libertad para los términos. Los términos no incluyen la constante. |
