En este tema
Suma de los cuadrados (SC)
En términos de matriz, estas son las fórmulas para las diferentes sumas de cuadrados:



Minitab desglosa el componente SC Regresión o SC Tratamientos en la cantidad de variación explicada por cada término utilizando tanto la suma de cuadrados secuenciales como la suma de cuadrados ajustados.
Notación
| Término | Description |
|---|---|
| b | vector de coeficientes |
| X | matriz de diseño |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| J | n entre n matriz de 1s |
Suma secuencial de los cuadrados
Minitab desglosa el componente SC Regresión o Tratamientos de la varianza en las sumas secuenciales de los cuadrados para cada factor. Las sumas secuenciales de los cuadrados dependen del orden en que los factores o predictores se ingresan en el modelo. Las sumas secuenciales de cuadrados es la porción única de la SC Regresión explicada por un factor, dados los factores ingresados previamente.
Por ejemplo, si se tiene un modelo con tres factores o predictores, X1, X2 y X3, la suma secuencial de cuadrados para X2 muestra qué proporción de la variación restante puede explicar X2, dado que X1 ya se encuentra en el modelo. Para obtener una secuencia diferente de factores, repita el análisis e ingrese los factores en un orden diferente.
Grados de libertad (GL)
Los grados de libertad para cada componente del modelo son:
| Fuentes de variación | GL |
|---|---|
| Regresión | p |
| Error | n – p – 1 |
| Total | n – 1 |
- Los datos contienen múltiples observaciones con los mismos valores predictores.
- Los datos contienen los puntos correctos para estimar términos adicionales que no están en el modelo.
Notación
| Término | Description |
|---|---|
| n | número de observaciones |
| p | número de coeficientes en el modelo, sin contar la constante |
CM ajust – Regresión
La fórmula del cuadrado medio (CM) de la regresión es:
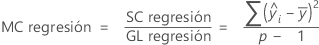
Notación
| Término | Description |
|---|---|
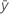 | respuesta media |
 | iésima respuesta ajustada |
| p | número de términos en el modelo |
CM ajustado – Error
El cuadrado medio del error (también abreviado como CM error o MSE y conocido como s2) es la varianza alrededor de la línea de regresión ajustada. La fórmula es:
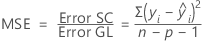
Notación
| Término | Description |
|---|---|
| yi | iésimo valor de respuesta observado |
 | iésima respuesta ajustada |
| n | número de observaciones |
| p | número de coeficientes en el modelo, sin contar la constante |
CM Ajust. – Total
La fórmula para el cuadrado medio (CM) total es:
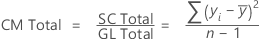
Notación
| Término | Description |
|---|---|
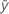 | respuesta media |
| yi | valor de la iésima respuesta observada |
| n | número de observaciones |
Valor F
Las fórmulas para el estadístico F son las siguientes:
- F(Regresión)
-
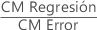
- F(Término)
-

- F(Falta de ajuste)
-

Notación
| Término | Description |
|---|---|
| CM Regresión | Una medida de la variación en la respuesta que explica el modelo actual. |
| CM Error | Una medida de la variación que el modelo no explica. |
| CM Término | Una medida de la cantidad de variación que un término explica después de justificar los otros términos incluidos en el modelo. |
| CM Falta de ajuste | Una medida de la variación en la respuesta que podría modelarse al agregar más términos al modelo. |
| CM Error puro | Una medida de la variación en los datos de respuesta replicados. |
Valor p – Tabla Análisis de varianza
El valor p es una probabilidad que se calcula a partir de una distribución F con los grados de libertad (GL) que se indican a continuación:
- GL del numerador
- suma de los grados de libertad para el término o los términos en la prueba
- GL del denominador
- grados de libertad para el error
Fórmula
1 − P(F ≤ fj)
Notación
| Término | Description |
|---|---|
| P(F ≤ f) | función de distribución acumulada para la distribución F |
| f | estadístico F para la prueba |
Prueba de falta de ajuste de error puro
- La suma de las desviaciones al cuadrado de la respuesta con respecto a la media en cada conjunto de réplicas y las suma juntas para crear la suma de los cuadrados del error puro (SC EP).
- El cuadrado medio del error puro


donde n = número de observaciones y m = número de distintas combinaciones del nivel x
- La suma de los cuadrados de la falta de ajuste

- El cuadrado medio de la falta de ajuste

- Los estadísticos de prueba

Los valores F y los valores p pequeños sugieren que el modelo es inadecuado.
Valor p – Prueba de falta de ajuste
- GL del numerador
- grados de libertad para la falta de ajuste
- GL del denominador
- grados de libertad para el error puro
Fórmula
1 − P(F ≤ fj)
Notación
| Término | Description |
|---|---|
| P(F ≤ fj) | función de distribución acumulada para la distribución F |
| fj | estadístico F para la prueba |
