En este tema
R-cuad. de desviación
El R2 de desviación por lo general es considerado la proporción de la desviación total en la variable de respuesta que el modelo explica.
Interpretación
Mientras más alta sea la desviación R2, mejor se ajustará el modelo a los datos. La desviación de R2 siempre se encuentra entre 0% y 100%.
El R2 de desviación siempre se incrementa cuando usted agrega términos adicionales a un modelo. Por ejemplo, el mejor modelo de 5 términos siempre tendrá un R2 que sea al menos tan alto como el mejor modelo de 4 modelos. Por lo tanto, el R2 de desviación es más útil cuando se comparan modelos del mismo tamaño.
Los estadísticos de bondad de ajuste son simplemente una medida de qué tan bien se ajusta el modelo a los datos. Incluso cuando un modelo tenga un valor deseable, usted deberá revisar las gráficas de residuos y las pruebas de bondad de ajuste para evaluar qué tan bien se ajusta un modelo a los datos.
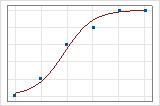
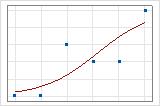
Puede utilizar una gráfica de línea ajustada para ilustrar gráficamente diferentes valores del R2 de desviación. La primera gráfica ilustra un modelo que explica aproximadamente 96% de la desviación en la respuesta. La segunda gráfica ilustra un modelo que explica aproximadamente 60% de la desviación en la respuesta. Mientras mayor sea la desviación explicada por un modelo, más cerca de la curva estarán los puntos de los datos. Teóricamente, si un modelo pudiera explicar el 100% de la desviación, los valores ajustados siempre serían iguales a los valores observados y todos los puntos de los datos estarían sobre la curva.
La organización de los datos afecta el valor de R2 de desviación. El R2 de desviación suele ser más alto para datos con múltiples pruebas por fila que para datos con una sola prueba por fila. Los valores de R2 de desviación son comparables solamente entre modelos que utilizan el mismo formato de datos. Para obtener más información, vaya a Cómo los formatos de datos afectan la bondad de ajuste en regresión logística binaria.
R-cuad. de desviación (ajust.)
La desviación ajustada de R2 es la proporción de desviación en la respuesta que es explicada por el modelo, ajustado para el número de predictores en el modelo relativo al número de observaciones.
Interpretación
Utilice el R2 de desviación ajustado para comparar modelos que tengan diferentes números de términos. El R2 de desviación siempre se incrementa cuando usted agrega un término al modelo. El valor ajustado de R2 de desviación incorpora el número de términos en el modelo como ayuda para elegir el modelo correcto.
| Paso | % Patata | Tasa de enfriamiento | Temp. de cocción | R2 de desviación | R2 de desviación ajustado | Valor p |
|---|---|---|---|---|---|---|
| 1 | X | 52% | 51% | 0.000 | ||
| 1 | X | X | 63% | 62% | 0.000 | |
| 3 | X | X | X | 65 | 62 | 0.000 |
El primer paso produce un modelo de regresión estadísticamente significativo. El segundo paso, que agrega la tasa de enfriamiento al modelo, aumenta el R2 de desviación ajustado, lo que indica que la tasa de enfriamiento mejora el modelo. El tercer paso, que agrega la temperatura de cocción al modelo, aumenta el R2 de desviación, pero no el R2 de desviación ajustado. Estos resultados indican que la temperatura de cocción no mejora el modelo. Con base en estos resultados, considere eliminar la temperatura de cocción del modelo.
La organización de los datos afecta el valor de R2 de desviación ajustado. Para los mismos datos, el R2 de desviación ajustado suele ser más alto para datos con múltiples pruebas por fila que para datos con una sola prueba por fila. Utilice el R2 de desviación ajustado solo para comparar el ajuste de modelos que tengan el mismo formato de datos. Para obtener más información, vaya a Cómo los formatos de datos afectan la bondad de ajuste en regresión logística binaria.
R-cuad. de la Desviación de prueba
Interpretación
Utilice el R2 de la desviación de prueba para determinar qué tan bien se ajusta el modelo a los nuevos datos. Los modelos que tienen valores de R2 de la desviación más grandes tienden a funcionar mejor con nuevos datos. Puede utilizar el R2 de la desviación de prueba para comparar el rendimiento de diferentes modelos.
Un R2 de la desviación de prueba que es sustancialmente menor que el R2 de la desviación puede indicar que el modelo está demasiado ajustado. Un modelo con ajuste excesivo se produce cuando se agregan términos para efectos que no son importantes en la población. El modelo se adapta a los datos de entrenamiento y, por lo tanto, puede no ser útil para hacer predicciones sobre la población.
Por ejemplo, un analista de una empresa de consultoría financiera desarrolla un modelo para predecir las condiciones futuras del mercado. El modelo parece prometedor porque tiene un R2 del 87%. Sin embargo, el R2 de la desviación de prueba es del 52%, lo que indica que el modelo podría estar demasiado ajustado.
Un valor alto de R2 de la desviación no indica por sí mismo que el modelo cumple con los supuestos del modelo. Debe comprobar las gráficas de residuos para verificar los supuestos.
R-cuad. de desviación de K pliegues
El R2 de la desviación de K pliegues se considera generalmente la proporción de la desviación total en la variable de respuesta de los datos de validación que explica el modelo.
Interpretación
Utilice el R2 de la desviación de K pliegues para determinar qué tan bien se ajusta el modelo a los nuevos datos. Los modelos que tienen valores R2 de la desviación de K pliegues más grandes tienden a funcionar mejor con nuevos datos. Puede utilizar valores R2 de la desviación de K pliegues para comparar el rendimiento de diferentes modelos.
Un R2 de la desviación de K pliegues que es sustancialmente menor que el R2 de la desviación puede indicar que el modelo está demasiado ajustado. Un modelo con ajuste excesivo se produce cuando se agregan términos para efectos que no son importantes en la población. El modelo se adapta al conjunto de datos de entrenamiento y, por lo tanto, puede no ser útil para hacer predicciones sobre la población.
Por ejemplo, un analista de una empresa de consultoría financiera desarrolla un modelo para predecir las condiciones futuras del mercado. El modelo parece prometedor porque tiene un R2 de la desviación de 87%. Sin embargo, el R2 de la desviación de K pliegues es 52%, lo que indica que el modelo podría estar demasiado ajustado.
Un valor alto de R2 de la desviación de K pliegues por sí mismo no indica que el modelo cumpla con los supuestos del modelo. Debe comprobar las gráficas de residuos para verificar los supuestos.
AIC, AICc and BIC
El criterio de información de Akaike (AIC), el criterio de información de Akaike corregido (AICc) y el criterio de información bayesiano (BIC) son medidas de la calidad relativa de un modelo que representan el ajuste y el número de términos en el modelo.
Interpretación
- AICc y AIC
- Cuando el tamaño de la muestra es pequeño en relación con los parámetros incluidos en el modelo, el AICc tiene un mejor desempeño que el AIC. El AICc tiene un mejor desempeño debido a que, con tamaños de muestras relativamente pequeños, el AIC tiende a ser pequeño para modelos con demasiados parámetros. Por lo general, los dos estadísticos dan resultados similares cuando el tamaño de la muestra es suficientemente grande en relación con los parámetros incluidos en el modelo.
- AICc y BIC
- Tanto el AICc como el BIC evalúan la probabilidad del modelo y luego aplican una penalización por agregar términos al modelo. La penalización reduce la tendencia a sobreajustar el modelo a los datos de la muestra. Esta reducción puede producir un modelo que tenga un mejor desempeño en general.
