A un ingeniero especializado en calidad le preocupan dos tipos de defectos en piezas moldeadas de resina: decoloración y formación de grumos. Las rayas descoloridas en el producto final pueden deberse a la contaminación de las mangueras y la abrasión de los gránulos de resina. La formación de grumos puede ocurrir cuando el proceso se ejecuta a temperaturas más altas y a mayores velocidades de transferencia. El ingeniero identifica tres posibles variables predictoras para las respuestas (defectos). El ingeniero registra el número de cada tipo de defecto en sesiones de una hora, mientras varía los niveles de los predictores.
El ingeniero desea estudiar de qué manera varios predictores afectan los defectos de decoloración. Puesto que la variable de respuesta describe el número de veces que ocurre un evento en un espacio finito de observación, el ingeniero ajusta un modelo de Poisson.
- Ingrese los datos de muestra, DefectosResina.MWX.
- Elija .
- En Respuesta, ingrese “Def. descoloración”.
- En Predictores continuos, ingrese 'Horas desde limpieza' Temperatura.
- En Predictores categóricos, ingrese “Tamaño del tornillo”.
- Haga clic en Gráficas.
- En Residuos para gráficas, seleccione Estandarizado.
- En Gráficas de residuos, seleccione Cuatro en uno.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
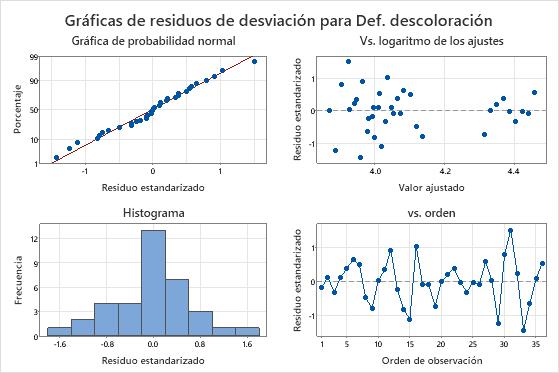
La gráfica de los residuos estandarizados de desviación versus los valores ajustados muestra una curva acentuada. En la gráfica de los residuos versus el orden, los residuos que se encuentran en el centro tienden a ser más altos que los residuos que están al principio y al final del conjunto de datos. Para estos datos, ambos patrones se deben a un término de interacción faltante entre el tamaño del tornillo y la temperatura. El patrón se puede ver en la gráfica de los residuales versus el orden, porque el ingeniero no recolectó los datos en orden aleatorio. El ingeniero vuelve a ajustar el modelo con la interacción entre la temperatura y el tamaño del tornillo para modelar los defectos con mayor exactitud.
Método
| Función de enlace | Logaritmo natural |
|---|---|
| Codificación de predictores categóricos | (1, 0) |
| Filas utilizadas | 36 |
Ecuación de regresión
| Def. descoloración | = | exp(Y') |
|---|
| Tamaño del tornillo | |||
|---|---|---|---|
| grande | Y' | = | 4.398 + 0.01798 Horas desde limpieza - 0.001974 Temperatura |
| pequeño | Y' | = | 4.244 + 0.01798 Horas desde limpieza - 0.001974 Temperatura |
Coeficientes
| Término | Coef | EE del coef. | Valor Z | Valor p | FIV |
|---|---|---|---|---|---|
| Constante | 4.3982 | 0.0628 | 70.02 | 0.000 | |
| Horas desde limpieza | 0.01798 | 0.00826 | 2.18 | 0.029 | 1.00 |
| Temperatura | -0.001974 | 0.000318 | -6.20 | 0.000 | 1.00 |
| Tamaño del tornillo | |||||
| pequeño | -0.1546 | 0.0427 | -3.62 | 0.000 | 1.00 |
Resumen del modelo
| R-cuadrado de la Desviación | R-cuadrado de la Desviación (ajust) | AIC | AICc | BIC |
|---|---|---|---|---|
| 64.20% | 60.80% | 253.29 | 254.58 | 259.62 |
Pruebas de bondad de ajuste
| Prueba | GL | Estimar | Media | Chi-cuadrada | Valor p |
|---|---|---|---|---|---|
| Desviación | 32 | 31.60722 | 0.98773 | 31.61 | 0.486 |
| Pearson | 32 | 31.26713 | 0.97710 | 31.27 | 0.503 |
Análisis de Varianza
| Prueba de Wald | |||
|---|---|---|---|
| Fuente | GL | Chi-cuadrada | Valor p |
| Regresión | 3 | 56.29 | 0.000 |
| Horas desde limpieza | 1 | 4.74 | 0.029 |
| Temperatura | 1 | 38.46 | 0.000 |
| Tamaño del tornillo | 1 | 13.09 | 0.000 |
Ajustes y diagnósticos para observaciones poco comunes
| Obs | Def. descoloración | Ajuste | Resid | Resid est. | |
|---|---|---|---|---|---|
| 33 | 43.00 | 58.18 | -2.09 | -2.18 | R |
- Presiones Ctrl+E o haga clic en el botón Editar último cuadro de diálogo
 en la barra de herramientas Estándar.
en la barra de herramientas Estándar. - Haga clic en Modelo.
- En Predictores, seleccione Temperatura y 'Tamaño del tornillo'.
- Al lado de Interacciones hasta el orden, elija 2 y haga clic en Agregar.
- Haga clic en Aceptar en cada cuadro de diálogo.
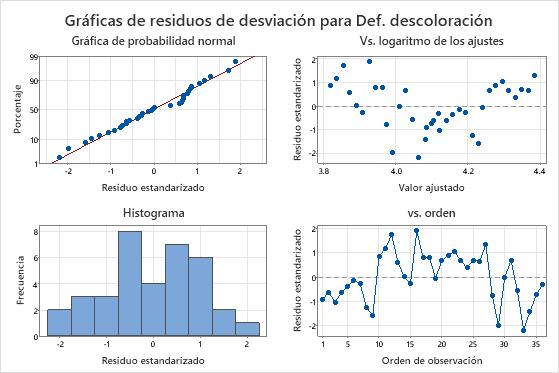
Para el modelo que incluye la interacción, el AIC es aproximadamente 236, que es más bajo que el del modelo sin la interacción. El criterio AIC indica que el modelo que incluye la interacción es mejor que el modelo que no la incluye. La curvatura en la gráfica de los residuos versus los ajustes ya no se observa. El ingeniero nota que algunos coeficientes tienen valores VIF que son > 5. En este caso, un análisis con predictores continuos estandarizados para reducir el efecto de la colinealidad arroja las mismas conclusiones sobre la significación estadística de los términos en el modelo. (Para obtener más información, vaya a Multicolinealidad en regresión.) El ingeniero decide interpretar este modelo en lugar del modelo sin la interacción.
Método
| Función de enlace | Logaritmo natural |
|---|---|
| Codificación de predictores categóricos | (1, 0) |
| Filas utilizadas | 36 |
Ecuación de regresión
| Def. descoloración | = | exp(Y') |
|---|
| Tamaño del tornillo | |||
|---|---|---|---|
| grande | Y' | = | 4.576 + 0.01798 Horas desde limpieza - 0.003285 Temperatura |
| pequeño | Y' | = | 4.032 + 0.01798 Horas desde limpieza - 0.000481 Temperatura |
Coeficientes
| Término | Coef | EE del coef. | Valor Z | Valor p | FIV |
|---|---|---|---|---|---|
| Constante | 4.5760 | 0.0736 | 62.15 | 0.000 | |
| Horas desde limpieza | 0.01798 | 0.00826 | 2.18 | 0.029 | 1.00 |
| Temperatura | -0.003285 | 0.000441 | -7.46 | 0.000 | 1.92 |
| Tamaño del tornillo | |||||
| pequeño | -0.5444 | 0.0990 | -5.50 | 0.000 | 5.37 |
| Temperatura*Tamaño del tornillo | |||||
| pequeño | 0.002804 | 0.000640 | 4.38 | 0.000 | 6.64 |
Resumen del modelo
| R-cuadrado de la Desviación | R-cuadrado de la Desviación (ajust) | AIC | AICc | BIC |
|---|---|---|---|---|
| 85.99% | 81.46% | 236.05 | 238.05 | 243.97 |
Pruebas de bondad de ajuste
| Prueba | GL | Estimar | Media | Chi-cuadrada | Valor p |
|---|---|---|---|---|---|
| Desviación | 31 | 12.36598 | 0.39890 | 12.37 | 0.999 |
| Pearson | 31 | 12.31611 | 0.39729 | 12.32 | 0.999 |
Análisis de Varianza
| Prueba de Wald | |||
|---|---|---|---|
| Fuente | GL | Chi-cuadrada | Valor p |
| Regresión | 4 | 78.77 | 0.000 |
| Horas desde limpieza | 1 | 4.74 | 0.029 |
| Temperatura | 1 | 55.60 | 0.000 |
| Tamaño del tornillo | 1 | 30.21 | 0.000 |
| Temperatura*Tamaño del tornillo | 1 | 19.17 | 0.000 |