En este tema
Coeficientes
Existen dos métodos para encontrar las estimaciones de máxima verosimilitud de los coeficientes. Un método es maximizar directamente la función de verosimilitud con respecto a los coeficientes. Estas expresiones son no lineales en los coeficientes. El método alternativo es utilizar un enfoque iterativo de mínimos cuadrados repesados (IRWLS), que es el método que Minitab utiliza para obtener las estimaciones de los coeficientes. McCullagh y Nelder1 muestran que los dos métodos son equivalentes. Sin embargo, el método iterativo de mínimos cuadrados reponderados es más fácil de implementar. Para obtener detalles, véase 1.
Método de aproximación de un solo paso para algunos casos de validación cruzada k-fold
Para algunos diseños de muestra grande con muchos pliegues de validación cruzada, Minitab utiliza un método de aproximación de un solo paso en el algoritmo de validación cruzada para disminuir el tiempo de cálculo (consulte Pregibon2 y Williams3). Para estos diseños, en lugar de ajustar el modelo de entrenamiento para un pliegue con el algoritmo IRWLS a plena convergencia, las estadísticas de validación cruzada para el pliegue provienen de los parámetros de regresión del primer paso iterativo del algoritmo.
En la tabla siguiente se muestran los diseños que obtienen estadísticas de validación cruzada de la aproximación de 1 paso.
| Tamaño de la muestra (n) | Número de columnas en la matriz de diseño (p) | Número de pliegues (k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p > 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p > 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p 50 | k > 1,000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p > 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p > 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p > 150 | k > 20 | |
| n > 100.000 | Cualquier valor de p | k > 100 |
Algoritmo de aproximación de un solo paso
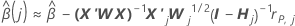
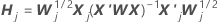
Notación
| Término | Description |
|---|---|
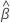 | los coeficientes estimados se ajustan al conjunto de datos completo |
| X | la matriz de diseño para el conjunto de datos completo |
| X' | el transversal de la matriz de diseño para el conjunto de datos completo |
| W | la matriz de peso para el conjunto de datos completo |
| X'j | la matriz de diseño de los datos en eljth fold |
| Wj | la matriz de peso para los datos en eljth fold |
| Yo | la matriz de identidad |
| rp, j | el vector de residuos de Pearson del modelo para el conjunto de datos completo para los datos en el jth fold |
[1] P. McCullagh y J. A. Nelder (1989). Modelos Lineales Generalizados,2nd Ed., Chapman & Hall/CRC, Londres.
[2] D. Pregibon (1981). Diagnóstico de regresión logística. The Annals of Statistics, 9(4), 705-724.
[3] D. A. Williams (1987). Diagnóstico de modelos lineales generalizados utilizando la desviación y eliminaciones de casos individuales, Estadísticas aplicadas, 36(2), 181-191.
Error estándar de coeficientes
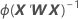
W es una matriz diagonal donde los elementos diagonales vienen dados por la siguiente fórmula:
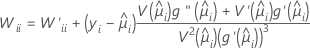
donde

Esta matriz de varianzas-covarianzas se basa en la matriz hessiana observada en contraposición a la matriz de información de Fisher. Minitab utiliza la matriz hessiana observada porque el modelo resultante es más robusto ante cualquier especificación errónea condicional de la media.
Si se utiliza el enlace canónico, entonces la matriz hessiana observada y la matriz de información de Fisher son idénticas.
Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para la iésima fila |
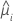 | la respuesta media estimada para la iésima fila |
| V(·) | la función de varianza especificada en la siguiente tabla |
| g(·) | la función de enlace |
| V '(·) | la primera derivada de la función de varianza |
| g'(·) | la primera derivada de la función de enlace |
| g''(·) | la segunda derivada de la función de enlace |
La función de varianza depende del modelo:
| Modelo | Función de varianza |
| Binomial | 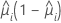 |
| Poisson | 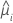 |
Para obtener más información, véase [1] y [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
El estadístico Z se utiliza para determinar si el predictor está significativamente relacionado con la respuesta. Los valores absolutos más grandes de Z indican una relación significativa. La fórmula es:
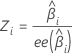
Notación
| Término | Description |
|---|---|
| Zi | El estadístico de prueba para una distribución normal estándar |
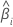 | El coeficiente estimado |
 | El error estándar del coeficiente estimado |
Para muestras pequeñas, la prueba de relación de probabilidades puede ser una prueba de significancia más fiable. Los valores p de relación de probabilidades están en la tabla Desviación. Cuando el tamaño de la muestra es lo suficientemente grande, los valores p de los estadísticos Z se aproximan a los valores p de los estadísticos de relación de probabilidades.
Valor p (P)
Se utilizan en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula. El valor p es la probabilidad de obtener un estadístico de prueba que sea por lo menos tan extremo como el valor real calculado, si la hipótesis nula es verdadera. Un valor de corte que se utiliza comúnmente para el valor p es 0.05. Por ejemplo, si el valor p calculado de un estadístico de prueba es menor que 0.05, usted rechaza la hipótesis nula.
Relación de probabilidades para la regresión logística binaria
La relación de probabilidades se proporciona solo si usted selecciona la función de enlace logit para un modelo con una respuesta binaria. En este caso, la relación de probabilidades es útil para interpretar la relación entre un predictor y una respuesta.
La relación de probabilidades (τ) puede ser cualquier número no negativo. Una relación de probabilidades = 1 sirve como base para la comparación. Si τ = 1, no hay ninguna asociación entre la respuesta y el predictor. Si τ < 1, las probabilidades del evento son mayores para el nivel de referencia del factor (o para niveles más bajos de un predictor continuo). Si τ > 1, las probabilidades del evento son menores que el nivel de referencia del factor (o para niveles más bajos de un predictor continuo). Los valores más distantes de 1 representan grados de asociación más fuertes.
Nota
Para el modelo de regresión logística binaria con una covariable o factor, las probabilidades estimadas de éxito son:
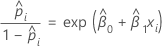
La relación exponencial proporciona una interpretación de β: Las probabilidades aumentan de manera multiplicativa en eβ1 por cada incremento de una unidad en x. La relación de probabilidades es equivalente a exp(β1).
Por ejemplo, si β es 0.75, la relación de probabilidades es exp(0.75), que es 2.11. Esto indica que hay un aumento de 111% en las probabilidades de éxito para cada aumento de una unidad en x.
Notación
| Término | Description |
|---|---|
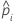 | la probabilidad estimada de un éxito para la iésima fila de los datos |
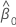 | el coeficiente estimado de la intersección |
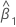 | el coeficiente estimado para el predictor x |
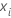 | el punto de los datos para la iésima fila |
Intervalo de confianza
El intervalo de confianza de un coeficiente estimado para una muestra grande es:
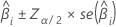
Para la regresión logística binaria, Minitab proporciona intervalos de confianza para las relaciones de probabilidades. Para obtener el intervalo de confianza de la relación de probabilidades, eleve a una potencia los límites inferior y superior del intervalo de confianza. El intervalo proporciona el rango en el que podrían situarse las probabilidades para cada cambio de una unidad en el predictor.
Notación
| Término | Description |
|---|---|
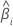 | el iésimo coeficiente |
 | la probabilidad acumulada inversa de la distribución normal estándar en 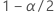 |
 | el nivel de significancia |
 | el error estándar del coeficiente estimado |
Matriz de varianzas-covarianzas
Una matriz de d x d, donde d es el número de predictores más uno. La varianza de cada coeficiente se encuentra en la celda diagonal y la covarianza de cada par de coeficientes se encuentra en la celda adecuada adyacente a la diagonal. La varianza es el error estándar del coeficiente elevado al cuadrado.
La matriz de varianzas-covarianzas se genera a partir de la última iteración de la inversa de la matriz de información. La matriz de varianzas-covarianzas tiene la siguiente forma:
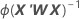
W es una matriz diagonal donde los elementos diagonales vienen dados por la siguiente fórmula:

donde

Esta matriz de varianzas-covarianzas se basa en la matriz hessiana observada en contraposición a la matriz de información de Fisher. Minitab utiliza la matriz hessiana observada porque el modelo resultante es más robusto ante cualquier especificación errónea condicional de la media.
Si se utiliza el enlace canónico, entonces la matriz hessiana observada y la matriz de información de Fisher son idénticas.
Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para la iésima fila |
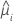 | la respuesta media estimada para la iésima fila |
| V(·) | la función de varianza especificada en la siguiente tabla |
| g(·) | la función de enlace |
| V '(·) | la primera derivada de la función de varianza |
| g'(·) | la primera derivada de la función de enlace |
| g''(·) | la segunda derivada de la función de enlace |
La función de varianza depende del modelo:
| Modelo | Función de varianza |
| Binomial | 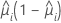 |
| Poisson | 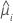 |
Para obtener más información, véase [1] y [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
