En este tema
- Residuos de Pearson
- Residuos estandarizados y eliminados de Pearson
- Residuos de Pearson estandarizados con validación
- Residuos de desviación
- Residuo estandarizado de desviación
- Residuo de desviación estandarizado con validación
- Residuo de desviación eliminado
- Delta chi-cuadrada
- Desviación delta
- Delta beta (estandarizado)
- Delta beta
- Apalancamientos
- Apalancamientos con validación
- Distancia de Cook
- DFITS
- Factor de inflación de la varianza (FIV)
Residuos de Pearson
Elementos de la chi-cuadrada de Pearson que se pueden utilizar para detectar patrones de factor/covariable mal ajustados. Minitab almacena el residuo de Pearson para el iésimo patrón de factor/covariable. La fórmula es:
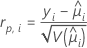
Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para el iésimo patrón de factor/covariable |
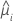 | el valor ajustado para el iésimo patrón de factor/covariable |
| V | la función de varianza para el modelo en 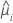 |
La función de varianza depende del modelo:
| Modelo | Función de varianza |
| Binomial | 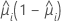 |
| Poisson | 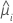 |
Residuos estandarizados y eliminados de Pearson
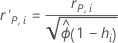
Notación
| Término | Description |
|---|---|
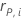 | el residuo de Pearson para el iésimo patrón de factor/covariable |
 | 1, para los modelos binomial y de Poisson |
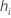 | el apalancamiento para el iésimo patrón de factor/covariable |
Residuos de Pearson estandarizados con validación
Fórmula
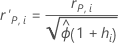
Notación
| Término | Description |
|---|---|
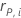
| the Pearson residual for the i-ésimo validation row |

| 1, for the binomial and Poisson models |
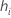 | the leverage for the i-ésimo validation row |
Residuos de desviación
Los residuos de desviación se basan en la desviación del modelo y son útiles para identificar los patrones de factor/covariable mal ajustados. La desviación del modelo es un estadístico de bondad de ajuste basado en la función de log-verosimilitud. El residuo de desviación definido para el iésimo patrón de factor/covariable es:

Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para el iésimo patrón de factor/covariable |
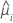 | el valor ajustado para el iésimo patrón de factor/covariable |
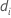 | la desviación para el iésimo patrón de factor/covariable |
Residuo estandarizado de desviación

Notación
| Término | Description |
|---|---|
| rD,i | El residuo de desviación para el iésimo patrón de factor/covariable |
| hi | El apalancamiento para el iésimo patrón de factor/covariable |
Residuo de desviación estandarizado con validación
Fórmula

Notación
| Término | Description |
|---|---|
| rD,i | The deviance residual for the i-ésimo validation row |
| hi | The leverage for the i-ésimo validation row |
Residuo de desviación eliminado

Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta en el iésimo patrón de factor/covariable |
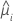 | el valor ajustado para el iésimo patrón de factor/covariable |
| hi | el apalancamiento para el iésimo patrón de factor/covariable |
| r'D,i | el residuo de desviación estandarizado para el iésimo patrón de factor/covariable |
| r'P,i | el residuo estandarizado de Pearson para el iésimo patrón de factor/covariable |
1. Pregibon, D. (1981). "Logistic Regression Diagnostics." The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.
Delta chi-cuadrada
Minitab calcula el cambio en la chi-cuadrada de Pearson debido a la eliminación de todas las observaciones con el jésimo patrón de factor/covariable. Minitab almacena un valor de delta chi-cuadrada para cada patrón distinto de factor/covariable en los datos. El valor de delta chi-cuadrada se puede utilizar para detectar patrones de factor/covariable mal ajustados. La fórmula para delta chi-cuadrada es:
Fórmula
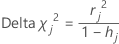
Notación
| Término | Description |
|---|---|
| hj | apalancamiento |
| rj | Residuos de Pearson |
Desviación delta
Minitab calcula el cambio en el estadístico de desviación eliminando todas las observaciones con el jésimo patrón de factor/covariable. Minitab almacena un valor para cada patrón distinto de factor/covariable en los datos. La desviación delta se puede utilizar para detectar patrones de factor/covariable mal ajustados. El cambio en el estadístico de desviación es:
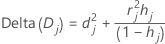
Notación
| Término | Description |
|---|---|
| hj | apalancamiento |
| rj | Residuos de Pearson |
| dj | residuos de desviación |
Delta beta (estandarizado)
Minitab calcula el cambio eliminando todas las observaciones con el jésimo patrón de factor/covariable. Se almacena un valor para cada patrón distinto de factor/covariable en los datos. Puede utilizar delta β estandarizado para detectar patrones de factor/covariable que tienen una gran influencia en las estimaciones de los coeficientes. Este valor se basa en el residuo estandarizado de Pearson.
Fórmula
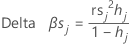
Notación
| Término | Description |
|---|---|
| hj | apalancamiento |
| rs j | residuos estandarizados de Pearson |
Delta beta
Minitab calcula el cambio eliminando todas las observaciones con el jésimo patrón de factor/covariable. Se almacena un valor para cada patrón distinto de factor/covariable en los datos. Puede utilizar β para detectar patrones de factor/covariable que tengan gran influencia en las estimaciones de los coeficientes. Este valor se basa en el residuo de Pearson.
Fórmula
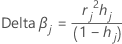
Notación
| Término | Description |
|---|---|
| hj | apalancamiento |
| rj | Residuos de Pearson |
Apalancamientos
Los apalancamientos son los elementos diagonales de la matriz de sombrero generalizada. Los apalancamientos son útiles para detectar patrones de factor/covariable que pueden tener una influencia significativa en los resultados.
Fórmula
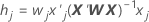
Notación
| Término | Description |
|---|---|
| wj | el jésimo elemento diagonal de la matriz de ponderaciones obtenida del ajuste de los coeficientes |
| xj | la jésima fila de la matriz de diseño |
| X | la matriz de diseño |
| X' | la transpuesta de X |
| W | la matriz de ponderaciones obtenida de la estimación de los coeficientes |
Apalancamientos con validación
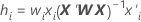
Notación
| Término | Description |
|---|---|
| wi | the internal weight for the i-ésimo validation row |
| xi | the row of the design matrix for the predictors in the i-ésimo validation row |
| X | the design matrix for the training data set |
| X' | the transpose of X |
| W | the diagonal matrix of internal weights for the training data set |
Distancia de Cook
Fórmula
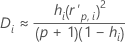
Notación
| Término | Description |
|---|---|
| hi | el apalancamiento para el iésimo patrón de factor/covariable |
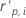 | el residuo estandarizado de Pearson para el iésimo patrón de factor/covariable |
| p | los grados de libertad para la regresión |
DFITS
Una medida de la influencia de una sola supresión en los valores ajustados. Las observaciones con valores grandes de DFITS pueden ser valores atípicos. Minitab calcula un valor aproximado para DFITS.
Fórmula

Notación
| Término | Description |
|---|---|
| hi | El apalancamiento para el punto de los datos |
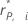 | El residuo eliminado de Pearson para el punto de los datos |
Factor de inflación de la varianza (FIV)

Notación
| Término | Description |
|---|---|
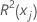 | el coeficiente de determinación con xj como la variable de respuesta y los otros términos del modelo como los predictores |
1. P. McCullagh y J. A. Nelder (1989). Generalized Linear Models, 2nd Edition, Chapman & Hall/CRC, London.
