En este tema
Familia exponencial y funciones de enlace
La extensión de los modelos lineales clásicos a modelos lineales generalizados consta de dos partes: una distribución de la familia exponencial y una función de enlace.
La familia exponencial
La primera parte extiende el modelo lineal a las variables de respuesta que son miembros de una familia grande de distribuciones llamada la familia exponencial. Los miembros de la familia exponencial de distribuciones tienen funciones de distribución de probabilidad para una respuesta observada con la siguiente forma general:
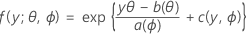
donde a(∙), b(∙) y c(∙) dependen de la distribución de la variable de respuesta. El parámetro θ es un parámetro de ubicación que suele mencionarse como el parámetro canónico y ϕ se denomina parámetro de dispersion. La función a(ϕ) por lo general tiene la forma a(ϕ)= ϕ/ ω, donde ω es una constante conocida o ponderación que puede variar de una observación a otra. (En Minitab, cuando se especifican ponderaciones, la función a(ϕ) se ajusta según corresponda.)
Los miembros de la familia exponencial pueden ser distribuciones discretas o distribuciones continuas. Las distribuciones normal y gamma son ejemplos de distribuciones continuas que son miembros de la familia exponencial. Las distribuciones binomial y de Poisson son ejemplos de distribuciones discretas que son miembros de la familia exponencial. La siguiente tabla contiene las características de algunas de estas distribuciones.
| Distribución | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| Normal | σ2 | θ2/2 | φω |  |
| Binomial | 1 | 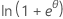 |
φ/ω | -ln(y!) |
| Poisson | 1 | exp(θ) | φ/ω |  |
La función de enlace
La segunda parte es la función de enlace. La función de enlace relaciona la media de la respuesta en la iésima observación con un predictor lineal que tiene esta forma:
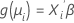
El modelo lineal clásico es un caso especial de esta formulación general donde la función de enlace es la función identidad.
La elección de la función de enlace en la segunda parte depende de la distribución específica de la familia exponencial de la primera parte. En particular, cada distribución de la familia exponencial tiene una función de enlace especial denominada función canónica de enlace. Esta función de enlace satisface la ecuación g (μi) = Xi'β= θ, donde θ es el parémetro canónico. La función canónica de enlace produce ciertas propiedades estadísticas deseables del modelo. Las estadísticas de bondad del ajuste se pueden usar para comparar ajustes utilizando diferentes funciones de enlace. Ciertas funciones de enlace se pueden utilizar por razones históricas o porque tienen un significado especial dentro de una disciplina. Por ejemplo, una ventaja de la función de enlace logit es que proporciona una estimación de las relaciones de probabilidades. Otro ejemplo es que la función de enlace normit presupone que hay una variable subyacente que sigue una distribución normal que se clasifica en categorías binarias.
Minitab provee tres funciones de enlace para cada clase de modelos. Las diferentes funciones de enlace permiten encontrar modelos que se ajustan adecuadamente a una variedad más amplia de datos.
Para los modelos binomiales, las funciones de enlace son logit, normit (también conocida como probit) y gompit (también denominada log-log complementario). Éstas son la inversa de la función de distribución logística acumulada estándar (logit), la inversa de la función de distribución normal acumulada estándar (normit) y la inversa de la función de distribución Gompertz (gompit). El logit es la función canónica de enlace para los modelos binomiales y, por lo tanto, el logit es la función de enlace predeterminada.
Para los modelos de Poisson, las funciones de enlace son el logaritmo natural, la raíz cuadrada y la identidad. El logaritmo natural es la función canónica de enlace para los modelos de Poisson y, por lo tanto, el logaritmo natural es la función de enlace predeterminada.
Las funciones de enlace se resumen a continuación:
| Modelo | Nombre | Función de enlace, g(μi) |
| Binomial | logit | 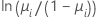 |
| Binomial | normit (probit) | 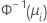 |
| Binomial | gompit (log-log complementario) |  |
| Poisson | logaritmo natural | 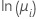 |
| Poisson | raíz cuadrada |  |
| Poisson | identidad | 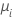 |
Notación
| Término | Description |
|---|---|
| μi | la respuesta media de la iésima fila |
| g(μi) | la función de enlace |
| X | el vector de las variables predictoras |
| β | el vector de los coeficientes asociado con los predictores |
 | la función de distribución acumulada inversa de la distribución normal |
Coeficientes
[1] P. McCullagh y J. A. Nelder (1989). Generalized Linear Models, 2nd Ed., Chapman & Hall/CRC, London.
Error estándar de coeficientes
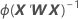
W es una matriz diagonal donde los elementos diagonales vienen dados por la siguiente fórmula:
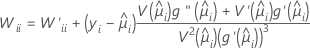
donde

Esta matriz de varianzas-covarianzas se basa en la matriz hessiana observada en contraposición a la matriz de información de Fisher. Minitab utiliza la matriz hessiana observada porque el modelo resultante es más robusto ante cualquier especificación errónea condicional de la media.
Si se utiliza el enlace canónico, entonces la matriz hessiana observada y la matriz de información de Fisher son idénticas.
Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para la iésima fila |
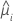 | la respuesta media estimada para la iésima fila |
| V(·) | la función de varianza especificada en la siguiente tabla |
| g(·) | la función de enlace |
| V '(·) | la primera derivada de la función de varianza |
| g'(·) | la primera derivada de la función de enlace |
| g''(·) | la segunda derivada de la función de enlace |
La función de varianza depende del modelo:
| Modelo | Función de varianza |
| Binomial | 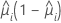 |
| Poisson | 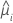 |
Para obtener más información, véase [1] y [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Relación de probabilidades para la regresión logística binaria
La relación de probabilidades se proporciona solo si usted selecciona la función de enlace logit para un modelo con una respuesta binaria. En este caso, la relación de probabilidades es útil para interpretar la relación entre un predictor y una respuesta.
La relación de probabilidades (τ) puede ser cualquier número no negativo. Una relación de probabilidades = 1 sirve como base para la comparación. Si τ = 1, no hay ninguna asociación entre la respuesta y el predictor. Si τ < 1, las probabilidades del evento son mayores para el nivel de referencia del factor (o para niveles más bajos de un predictor continuo). Si τ > 1, las probabilidades del evento son menores que el nivel de referencia del factor (o para niveles más bajos de un predictor continuo). Los valores más distantes de 1 representan grados de asociación más fuertes.
Nota
Para el modelo de regresión logística binaria con una covariable o factor, las probabilidades estimadas de éxito son:
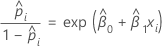
La relación exponencial proporciona una interpretación de β: Las probabilidades aumentan de manera multiplicativa en eβ1 por cada incremento de una unidad en x. La relación de probabilidades es equivalente a exp(β1).
Por ejemplo, si β es 0.75, la relación de probabilidades es exp(0.75), que es 2.11. Esto indica que hay un aumento de 111% en las probabilidades de éxito para cada aumento de una unidad en x.
Notación
| Término | Description |
|---|---|
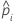 | la probabilidad estimada de un éxito para la iésima fila de los datos |
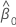 | el coeficiente estimado de la intersección |
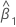 | el coeficiente estimado para el predictor x |
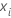 | el punto de los datos para la iésima fila |
Matriz de varianzas-covarianzas
Una matriz de d x d, donde d es el número de predictores más uno. La varianza de cada coeficiente se encuentra en la celda diagonal y la covarianza de cada par de coeficientes se encuentra en la celda adecuada adyacente a la diagonal. La varianza es el error estándar del coeficiente elevado al cuadrado.
La matriz de varianzas-covarianzas se genera a partir de la última iteración de la inversa de la matriz de información. La matriz de varianzas-covarianzas tiene la siguiente forma:
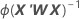
W es una matriz diagonal donde los elementos diagonales vienen dados por la siguiente fórmula:

donde

Esta matriz de varianzas-covarianzas se basa en la matriz hessiana observada en contraposición a la matriz de información de Fisher. Minitab utiliza la matriz hessiana observada porque el modelo resultante es más robusto ante cualquier especificación errónea condicional de la media.
Si se utiliza el enlace canónico, entonces la matriz hessiana observada y la matriz de información de Fisher son idénticas.
Notación
| Término | Description |
|---|---|
| yi | el valor de respuesta para la iésima fila |
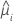 | la respuesta media estimada para la iésima fila |
| V(·) | la función de varianza especificada en la siguiente tabla |
| g(·) | la función de enlace |
| V '(·) | la primera derivada de la función de varianza |
| g'(·) | la primera derivada de la función de enlace |
| g''(·) | la segunda derivada de la función de enlace |
La función de varianza depende del modelo:
| Modelo | Función de varianza |
| Binomial | 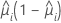 |
| Poisson | 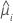 |
Para obtener más información, véase [1] y [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh y J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
