En este tema
Gráfica de línea ajustada binaria
La gráfica de líneas ajustadas muestra la respuesta y los datos del predictor. La gráfica incluye la línea de regresión que representa la ecuación de regresión. También puede elegir mostrar el intervalo de confianza para los valores ajustados.
Interpretación
Utilice la gráfica de línea ajustada para examinar la relación entre la variable de respuesta y la variable predictora.
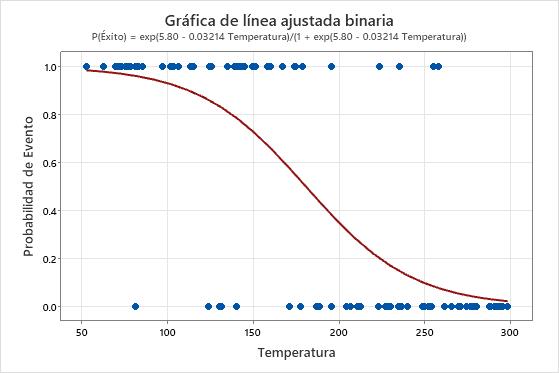
En estos resultados, la ecuación se escribe como la probabilidad de un éxito. El valor de respuesta de 1 en el eje Y representa un éxito. La gráfica muestra que la probabilidad de éxito disminuye a medida que la temperatura se incrementa. Cuando las temperaturas en los datos están cerca de 50, la pendiente de la línea no es muy abrupta, lo cual indica que la probabilidad de que disminuye lentamente a medida que la temperatura se incrementa. La línea es más inclinada en la porción media de los datos de temperatura, lo cual indica que un cambio de un grado en la temperatura tiene un efecto más grande en este rango. Cuando la probabilidad de éxito se aproxima a cero en el extremo alto del rango de temperatura, la línea se aplana de nuevo.
Si el modelo se ajusta adecuadamente a los datos, entonces las altas probabilidades de predicción muestran donde el evento es común. Cuando las temperaturas en los datos están cerca de 50, el valor de respuesta de 1 es más común. A medida que la temperatura aumenta, el valor de respuesta de cero pasa a ser más común.
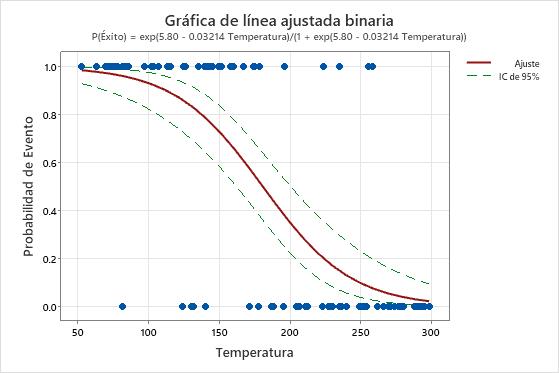
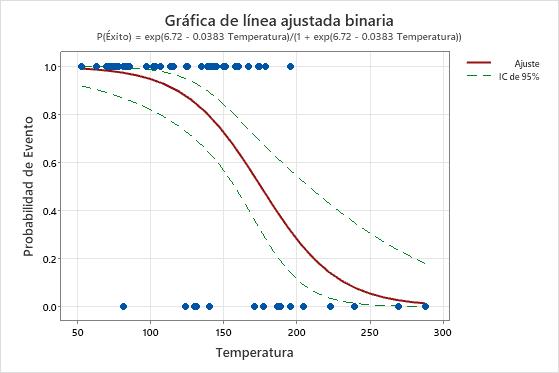
Si usted agrega intervalos de confianza a la gráfica, puede usar los intervalos para evaluar qué tan precisas son las estimaciones de los valores ajustados. En la primera de las siguientes gráficas, las líneas del intervalo de confianza son aproximadamente del mismo ancho a medida que el predictor aumenta. En la segunda gráfica, el intervalo de confianza se vuelve más amplio a medida que aumenta el valor del predictor. El intervalo amplio se debe en parte a la pequeña cantidad de datos cuando la temperatura es alta.
Histograma de residuos
El histograma de los residuos de desviación muestra la distribución de los residuos para todas las observaciones.
Interpretación
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Una larga cola en una dirección | Asimetría |
| Una barra que se encuentra muy alejada de las otras barras | Un valor atípico |
Puesto que la apariencia de un histograma depende del número de intervalos usados para agrupar los datos, no utilice un histograma para evaluar la normalidad de los residuos. En lugar de ello, utilice una gráfica de probabilidad normal.
Gráfica de probabilidad normal de los residuos
La gráfica de probabilidad normal de los residuos muestra los residuos vs. sus valores esperados cuando la distribución es normal.
Interpretación
Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
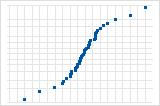
La curva S implica una distribución con colas largas.
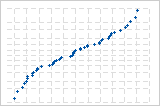
La curva S invertida implica una distribución con colas cortas.
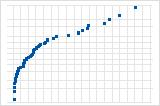
La curva descendente implica una distribución con asimetría a la derecha.
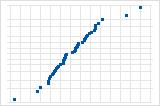
Algunos puntos alejados de la línea implican una distribución con valores atípicos.
Si observa un patrón no normal, utilice las otras gráficas de residuos para verificar otros problemas con el modelo, como términos faltantes o un efecto del orden cronológico. Si los residuos no siguen una distribución normal, los intervalos de confianza de la aproximación a la normal y los valores p de la prueba de Wald pueden ser inexactos.
Residuos vs. ajustes
La gráfica de residuos vs. ajustes muestra los residuos en el eje Y y los valores ajustados en el eje X. La gráfica es significativa cuando los datos están en formato Evento/Ensayo. Cuando los datos están en formato de Respuesta binaria/Frecuencia, Minitab no proporciona esta gráfica.
Interpretación
Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Una función de enlace inapropiada |
| Curvilíneo | Un término de orden superior faltante o una función de enlace inapropiada |
| Un punto que está alejado de cero | Un valor atípico |
| Un punto que está lejos de los otros puntos en la dirección x | Un punto influyente |

Gráfica con valor atípico
Uno de los puntos es mucho más grande que todos los otros puntos. Por lo tanto, el punto es un valor atípico. Si hay demasiados valores atípicos, el modelo podría no ser aceptable. Usted debe tratar de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). A continuación, repita el análisis.
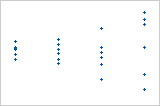
Gráfica con varianza no constante
La varianza de los residuos aumenta con los valores ajustados. Tenga en cuenta que, a medida que el valor de los ajustes aumenta, la dispersión entre los residuos se amplía. Este patrón indica que las varianzas de los residuos son desiguales (no constante).
| Problema | Posible solución |
|---|---|
| Varianza no constante | Considere utilizar diferentes términos en el modelo, una función de enlace diferente o ponderaciones. |
| Un valor atípico o punto de influencia |
|
Residuos vs. orden
La gráfica de residuos vs. orden muestra los residuos en el orden en que se recopilaron los datos.
Interpretación
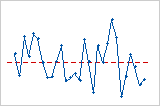
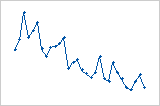
Tendencia
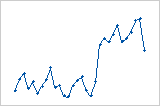
Cambio
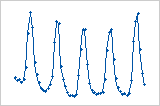
Ciclo
Residuos versus las variables
La gráfica residuos vs. las variables muestra los residuos versus otra variable. La variable pudiera estar ya incluida en el modelo. O, la variable podría no estar en el modelo, pero se sospecha que influye en la respuesta.
Interpretación
Si observa un patrón no aleatorio en los residuos, indica que la variable influye en la respuesta de forma sistemática. Considere incluir esta variable en un análisis.
