Métodos para Ajustar modelo y Descubrir predictores clave con Regresión TreeNet^®

Nota

Este comando está disponible con el Módulo de análisis predictivo. Haga doble clic aquí para obtener información sobre cómo activar el módulo.

Los modelos TreeNet^® son un enfoque para resolver problemas de clasificación y regresión que son más precisos y resistentes al sobreajuste que una clasificación individual o un árbol de regresión. La descripción amplia y general del proceso sería que comenzamos con un árbol de regresión pequeño como modelo inicial. De ese árbol provienen los residuos para cada fila de los datos que se convierten en la variable de respuesta para el siguiente árbol de regresión. A continuación, construimos otro árbol de regresión pequeño para predecir los residuos del primer árbol y se calculan los residuos resultantes nuevamente. Repetimos esta secuencia hasta que se identifica un número óptimo de árboles con un mínimo error de predicción utilizando un método de validación. La secuencia resultante de árboles conforma el modelo de regresión TreeNet^®.

Para el caso de la regresión, podemos añadir una descripción general del análisis, pero algunos detalles dependen de cuál de los siguientes es la función de pérdida:

Table 1. Valores para la función de pérdida del error cuadrático
Estadística	Valor
Ajuste inicial,	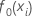media de la variable de respuesta
Residuo generalizado, 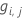como valor de respuesta para la fila i
Dentro de las actualizaciones de nodos,	media de

Table 2. Valores para la función de pérdida de la desviación absoluta
Estadística	Valor
Ajuste inicial,	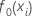mediana de la variable de respuesta
Residuo generalizado, 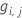como valor de respuesta para la fila i
Dentro de las actualizaciones de nodos,	mediana de

Función de pérdida Huber

Para la función de pérdida Huber, las estadísticas son las siguientes:

El ajuste inicial, 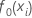, es igual a la mediana de todos los valores de respuesta.

Para ampliar el árbol jth,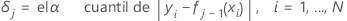

A continuación, el residuo generalizado para iésima fila es el siguiente:

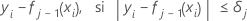
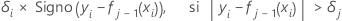
Los residuos generalizados se utilizan como valores de respuesta para ampliar el jésimo árbol.

El valor actualizado para las filas del mésimo nodo terminal del jésimo árbol es el siguiente:

Definir

para ser el residuo regular para la iésima fila después de ampliar los árboles j-1. Permita que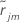

sea la mediana de

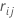los valores para las filas al interior del nodo terminal m del jésimo árbol. A continuación, el valor actualizado cada fila al interior del mésimo nodo terminal del jésimo árbol es:

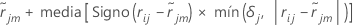
La media de la expresión anterior se calcula en todas las filas al interior del nodo terminal m del jésimo árbol.

Notación para funciones de pérdida

En los detalles anteriores, 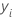es el valor de la variable de respuesta para la fila i, es el valor ajustado de los árboles j – 1 anteriores, y 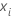es un vector que representa la i^ésima fila de los valores predictores en los datos de entrenamiento.

Parámetros de entrada

La creación del modelo también utiliza las siguientes entradas del analista:

Entrada	Símbolo
tasa de aprendizaje
tasa de muestreo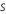
número máximo de nodos terminales por árbol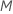
número de árboles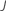
valor de cambio

Proceso general

El proceso tiene los siguientes pasos generales para ampliar el jésimo árbol, j = 1, ..., J:

Dibuje una muestra aleatoria de tamaño s * N a partir de los datos de entrenamiento, donde N es el número de filas en los datos de entrenamiento.
Calcule los residuos generalizados, 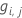, para .
Ajuste un árbol de regresión con no más de M nodos terminales a los residuos generalizados. El árbol divide las observaciones en no más de M grupos mutuamente excluyentes.
Para el m^ésimo nodo terminal en el árbol de regresión, calcule las actualizaciones dentro del nodo en relación con el árbol que dependen de la función de pérdida, .
Reduzca las actualizaciones dentro del nodo según la tasa de aprendizaje y aplique los valores para obtener los valores ajustados actualizados, :
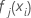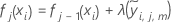
Repita los pasos del 1 al 5 para cada uno de los árboles J del análisis.