Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
Un equipo de investigadores quiere utilizar los datos de un proceso de moldeo por inyección para estudiar la configuración de las máquinas que maximizan un tipo de resistencia de una pieza de plástico. Las variables incluyen controles en las máquinas, diferentes fórmulas de plástico y las máquinas de moldeo por inyección.
Como parte de la exploración inicial de los datos, el equipo decide utilizar Descubrir predictores clave para comparar modelos mediante la eliminación secuencial de predictores sin importancia para identificar predictores clave. Los investigadores esperan identificar los predictores clave que tienen el mayor efecto en la respuesta y obtener más información sobre las relaciones entre la respuesta y los predictores clave.
- Abra el conjunto de datos de muestra proceso_de_inyección.MWX.
- Elija .
- En Respuesta, ingrese fuerza.
- En Predictores continuos, escriba 'presión de inyección' – 'temperatura a medida'.
- En Predictores categóricos, ingrese máquina y fórmula.
- Haga clic en Aceptar.
Interpretar los resultados
Para este análisis, Minitab Statistical Software compara 20 modelos. El asterisco de la columna Modelo de la tabla Evaluación del modelo muestra que el modelo con el mayor valor del estadístico R2 validado de forma cruzada es el modelo 16. El modelo 16 contiene 5 predictores importantes. Los resultados que siguen a la tabla de evaluación del modelo son para el modelo 16.
Aunque el modelo 16 tiene el mayor valor del estadístico R2 validado de forma cruzada, otros modelos tienen valores similares. El equipo puede hacer clic Seleccionar modelo alternativo para generar resultados para otros modelos desde la tabla Evaluación de modelos.
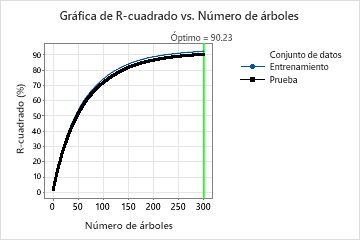
En los resultados del Modelo 16, la gráfica R cuadrado frente al número de árboles muestra que el número óptimo de árboles es igual al número de árboles en el análisis, 300. El equipo puede hacer clic Ajustar hiperparámetros para aumentar el número de árboles y ver si los cambios en otros hiperparámetros mejoran el rendimiento del modelo.
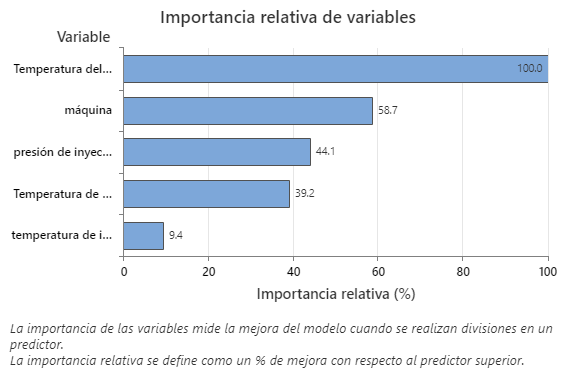
La gráfica Importancia relativa de las variables presenta los predictores en el orden de su efecto en la mejora del modelo cuando se realizan divisiones en un predictor sobre la secuencia de árboles. La variable predictora más importante es la temperatura del molde. Si la importancia de la principal variable predictora, la temperatura del molde, es del 100%, entonces la siguiente variable importante, la máquina, tiene una contribución del 58,7%. Esto significa que la máquina que inyecta es un 58,7% tan importante como la temperatura dentro del molde.
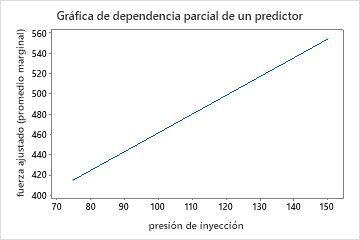
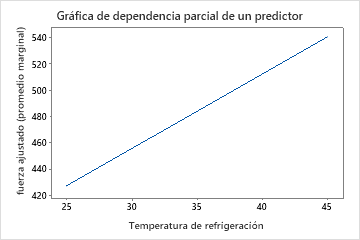
Utilice las gráficas de dependencia parcial para obtener información sobre cómo las variables o pares de variables importantes afectan la respuesta pronosticada. Las gráficas de dependencia parcial muestran si la relación entre la respuesta y una variable es lineal, monótona o más compleja.
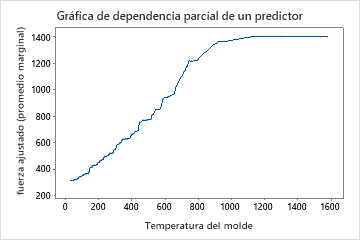
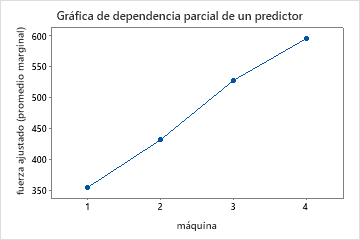
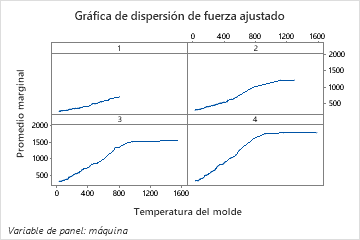
Los gráficos de dependencia parcial de un predictor muestran que la temperatura del molde, la presión de inyección y la temperatura de enfriamiento tienen una relación positiva con la resistencia. El gráfico de las máquinas muestra las diferencias entre las máquinas, con la máquina 1 fabricando las partes más débiles en promedio y la máquina 4 haciendo las partes más fuertes en promedio. El equipo se da cuenta de que la temperatura del molde y la máquina tienen la interacción más fuerte en los datos, por lo que observan el gráfico de dependencia parcial de dos predictores para comprender mejor cómo estas variables afectan la resistencia. El equipo puede seleccionar en los resultados producir gráficos para otras variables, como la temperatura de inyección.
El gráfico de dependencia parcial de dos predictores de la temperatura del molde y la máquina proporciona una idea de las diferentes resistencias medias de las máquinas. Una de las razones es que los datos de la máquina 1 no incluyen tantas observaciones a las temperaturas de molde más altas como las otras máquinas. El equipo aún podría decidir buscar otras razones por las que las máquinas producen diferentes resistencias cuando otras configuraciones son las mismas. El equipo puede hacer clic en los resultados para producir gráficos para otros pares de variables.
Método
| Función de pérdida | Error cuadrático |
|---|---|
| Criterio para seleccionar un número óptimo de árboles | R-cuadrado máximo |
| Validación del modelo | Validación cruzada de 3 pliegues |
| Tasa de aprendizaje | 0.01408 |
| Fracción de submuestra | 0.5 |
| Máximo de nodos terminales por árbol | 6 |
| Tamaño mínimo del nodo terminal | 3 |
| Número de predictores seleccionados para la división de nodos | Número total de predictores = 21 |
| Filas utilizadas | 1408 |
Información de respuesta
| Media | Desv.Est. | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 485.247 | 318.611 | 41.2082 | 301.099 | 398.924 | 562.449 | 2569.04 |
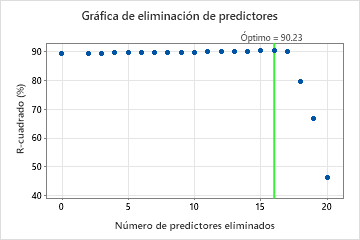
Selección del modelo eliminando predictores no importantes
| Modelo | Número óptimo de árboles | R-cuadrado (%) | Número de predictores | Predictores eliminados |
|---|---|---|---|---|
| 1 | 300 | 89.32 | 21 | Ninguno |
| 2 | 300 | 89.34 | 19 | caudal de plástico, cambiar de posición |
| 3 | 300 | 89.39 | 18 | Temperatura de secado |
| 4 | 300 | 89.46 | 17 | zona de temperatura de fusión 2 |
| 5 | 300 | 89.51 | 16 | Temperatura de plástico |
| 6 | 300 | 89.50 | 15 | fórmula |
| 7 | 300 | 89.59 | 14 | presión de retención |
| 8 | 300 | 89.57 | 13 | cojín de tornillo |
| 9 | 300 | 89.69 | 12 | zona de temperatura de fusión 4 |
| 10 | 300 | 89.70 | 11 | presión de espalda |
| 11 | 300 | 89.86 | 10 | zona de temperatura de fusión 1 |
| 12 | 300 | 89.90 | 9 | Tiempo de secado |
| 13 | 300 | 89.92 | 8 | temperatura a medida |
| 14 | 300 | 90.06 | 7 | zona de temperatura de fusión 5 |
| 15 | 300 | 90.16 | 6 | zona de temperatura de fusión 3 |
| 16* | 300 | 90.23 | 5 | Velocidad de rotación tornillo |
| 17 | 300 | 89.96 | 4 | temperatura de inyección |
| 18 | 297 | 79.37 | 3 | Temperatura de refrigeración |
| 19 | 244 | 66.64 | 2 | presión de inyección |
| 20 | 164 | 46.19 | 1 | máquina |
Resumen del modelo
| Total de predictores | 5 |
|---|---|
| Predictores importantes | 5 |
| Número de árboles cultivados | 300 |
| Número óptimo de árboles | 300 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
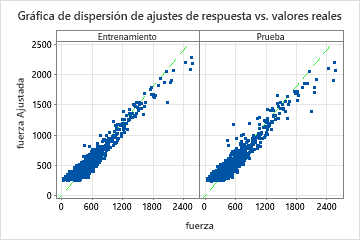
| R-cuadrado | 92.23% | 90.23% |
| Raíz de los cuadrados medios del error (RMSE) | 88.8049 | 99.5673 |
| Cuadrado medio del error (MSE) | 7886.3152 | 9913.6420 |
| Desviación absoluta media (MAD) | 68.9231 | 74.4113 |
| Media del error porcentual absoluto (MAPE) | 0.2083 | 0.2175 |