Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
Un equipo de investigadores quiere utilizar datos sobre un prestatario y la ubicación de una propiedad para predecir el monto de una hipoteca. Las variables incluyen los ingresos, la raza y el sexo del prestatario, así como la ubicación del área de censo de la propiedad, y otra información sobre el prestatario y el tipo de propiedad.
Después de la exploración inicial para Regresión CART® identificar los predictores importantes, el equipo ahora considera Regresión TreeNet® como un paso de seguimiento necesario. Los investigadores esperan obtener más información sobre las relaciones entre la respuesta y los predictores importantes y predecir nuevas observaciones con mayor exactitud.
Estos datos se adaptaron sobre la base de un conjunto de datos públicos que contiene información sobre las hipotecas de los bancos federales de préstamos para viviendas. Los datos originales son de fhfa.gov.
- Abra el conjunto de datos de muestra HipotecasCompradas.MTW.
- Elija .
- En Respuesta, ingrese Cant. préstamo.
- En Predictores continuos, escriba Ingreso anual – Ingreso del área.
- En Predictores categóricos, escriba Comprador primerizo – Área est. con núcleo.
- Haga clic en Validación.
- En Método de validación, seleccione Validación cruzada de K pliegues.
- En Número de pliegues (K), ingrese 3.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
Para este análisis, Minitab cultiva 300 árboles y el número óptimo de árboles es 300. Debido a que el número óptimo de árboles está cerca del número máximo de árboles que crece el modelo, los investigadores repiten el análisis con más árboles.
Resumen del modelo
| Total de predictores | 34 |
|---|---|
| Predictores importantes | 19 |
| Número de árboles cultivados | 300 |
| Número óptimo de árboles | 300 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| R-cuadrado | 94.02% | 84.97% |
| Raíz de los cuadrados medios del error (RMSE) | 32334.5587 | 51227.9431 |
| Cuadrado medio del error (MSE) | 1.04552E+09 | 2.62430E+09 |
| Desviación absoluta media (MAD) | 22740.1020 | 35974.9695 |
| Media del error porcentual absoluto (MAPE) | 0.1238 | 0.1969 |
Ejemplo con 500 árboles
- Seleccione Ajustar hiperparámetros en los resultados.
- En Número de árboles, ingrese 500.
- Haga clic en Mostrar resultados.
Interpretar los resultados
Para este análisis, hubo 500 árboles cultivados y el número óptimo de árboles para la combinación de hiperparámetros con el mejor valor del criterio de precisión es 500. La fracción de la submuestra cambia a 0.7 en lugar de 0.5 en el análisis original. La tasa de aprendizaje cambia a 0.0437 en lugar de 0.04372 en el análisis original.
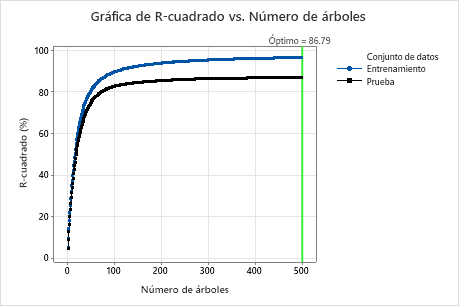
Examine tanto la tabla de resumen del modelo como el gráfico R-cuadrado vs Número de árboles. El valor de R2 cuando el número de árboles es 500 es 86.79% para los datos de prueba y es 96.41% para los datos de entrenamiento. Estos resultados muestran una mejoría con respecto a un análisis de regresión tradicional y un Regresión CART®.
Método
| Función de pérdida | Error cuadrático |
|---|---|
| Criterio para seleccionar un número óptimo de árboles | R-cuadrado máximo |
| Validación del modelo | Validación cruzada de 3 pliegues |
| Tasa de aprendizaje | 0.04372 |
| Fracción de submuestra | 0.5 |
| Máximo de nodos terminales por árbol | 6 |
| Tamaño mínimo del nodo terminal | 3 |
| Número de predictores seleccionados para la división de nodos | Número total de predictores = 34 |
| Filas utilizadas | 4372 |
Información de respuesta
| Media | Desv.Est. | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Método
| Función de pérdida | Error cuadrático |
|---|---|
| Criterio para seleccionar un número óptimo de árboles | R-cuadrado máximo |
| Validación del modelo | Validación cruzada de 3 pliegues |
| Tasa de aprendizaje | 0.001, 0.0437, 0.1 |
| Fracción de submuestra | 0.5, 0.7 |
| Máximo de nodos terminales por árbol | 6 |
| Tamaño mínimo del nodo terminal | 3 |
| Número de predictores seleccionados para la división de nodos | Número total de predictores = 34 |
| Filas utilizadas | 4372 |
Información de respuesta
| Media | Desv.Est. | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Optimización de hiperparámetros
| Modelo | Número óptimo de árboles | R-cuadrado (%) | Desviación absoluta media | Tasa de aprendizaje | Fracción de submuestra | Máximo de nodos terminales |
|---|---|---|---|---|---|---|
| 1 | 500 | 36.43 | 82617.1 | 0.0010 | 0.5 | 6 |
| 2 | 495 | 85.87 | 34560.5 | 0.0437 | 0.5 | 6 |
| 3 | 495 | 85.63 | 34889.3 | 0.1000 | 0.5 | 6 |
| 4 | 500 | 36.86 | 82145.0 | 0.0010 | 0.7 | 6 |
| 5* | 500 | 86.79 | 33052.6 | 0.0437 | 0.7 | 6 |
| 6 | 451 | 86.67 | 33262.3 | 0.1000 | 0.7 | 6 |
Resumen del modelo
| Total de predictores | 34 |
|---|---|
| Predictores importantes | 24 |
| Número de árboles cultivados | 500 |
| Número óptimo de árboles | 500 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| R-cuadrado | 96.41% | 86.79% |
| Raíz de los cuadrados medios del error (RMSE) | 25035.7243 | 48029.9503 |
| Cuadrado medio del error (MSE) | 6.26787E+08 | 2.30688E+09 |
| Desviación absoluta media (MAD) | 17309.3936 | 33052.6087 |
| Media del error porcentual absoluto (MAPE) | 0.0930 | 0.1790 |
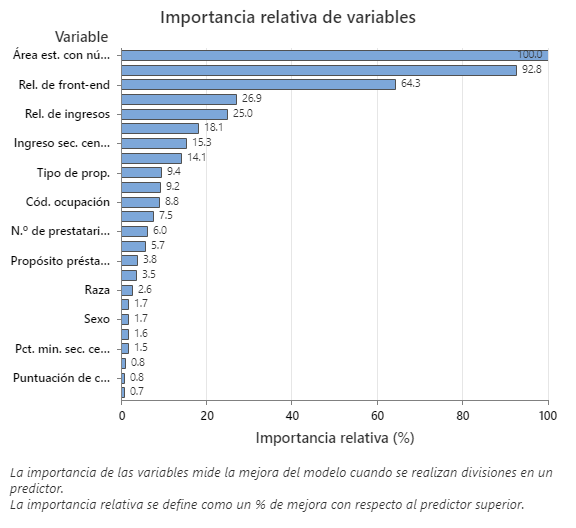
La gráfica Importancia relativa de las variables presenta los predictores en el orden de su efecto en la mejora del modelo cuando se realizan divisiones en un predictor sobre la secuencia de árboles. La variable predictora más importante es Área estadística basada en núcleo. Si la importancia de la variable predictora superior, el Área Estadística Basada en el Núcleo, es del 100%, entonces la siguiente variable importante, el Ingreso Anual, tiene una contribución del 92.8%. Esto significa que el ingreso anual del prestatario es 92.8% tan importante como la ubicación geográfica de la propiedad.
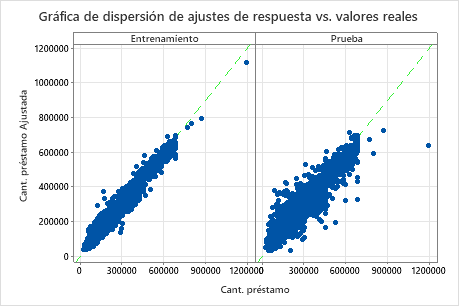
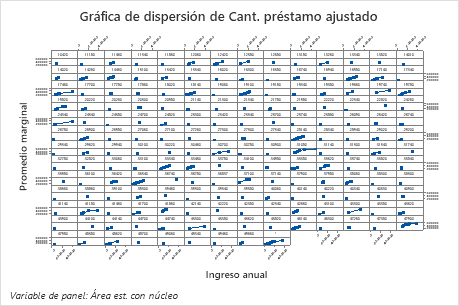
La gráfica de dispersión de las cantidades ajustadas de los préstamos vs. las cantidades reales de los préstamos muestra la relación entre los valores ajustados y reales tanto para los datos de entrenamiento como para los datos de prueba. Puede pasar el cursor sobre los puntos de la gráfica para ver más fácilmente los valores graficados. En este ejemplo, todos los puntos se encuentran aproximadamente cerca de la línea de referencia de y=x.
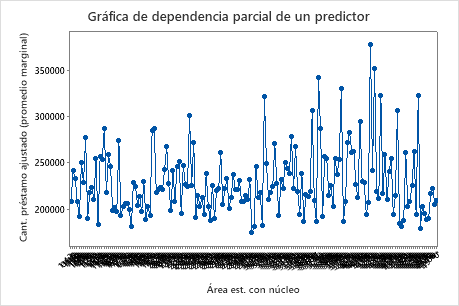
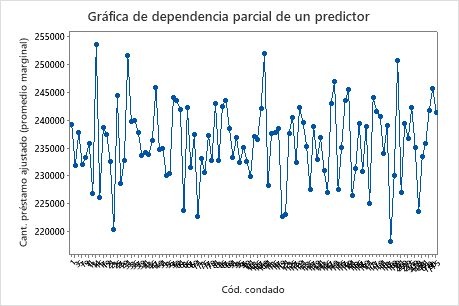
Utilice las gráficas de dependencia parcial para obtener información sobre cómo las variables o pares de variables importantes afectan los valores de respuesta ajustados. Las gráficas de dependencia parcial muestran si la relación entre la respuesta y una variable es lineal, monótona o más compleja.
La primera gráfica ilustra la cantidad ajustada del préstamo para cada área estadística basada en núcleo. Dado que hay tantos puntos de datos, puede pasar el cursor sobre puntos de datos individuales para ver los valores específicos de X y Y. Por ejemplo, el punto más alto en el lado derecho de la gráfica corresponde al área basada en núcleo número 41860 y la cantidad ajustada del préstamo es aproximadamente $378069
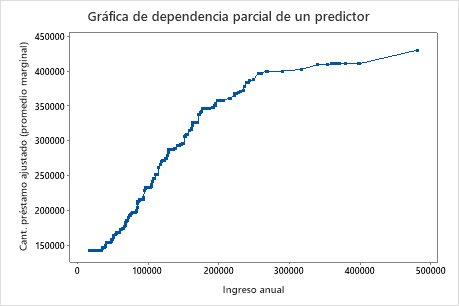
La segunda gráfica ilustra que la cantidad ajustada del préstamo aumenta a medida que aumenta el ingreso anual. Después de que el ingreso anual alcanza los $ 300000, los niveles de monto del préstamo ajustado aumentan a un ritmo más lento.
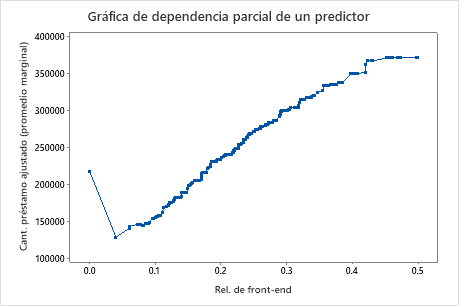
La tercera gráfica ilustra que el monto del préstamo ajustado aumenta a medida que aumenta la relación inicial.
El cuarto gráfico ilustra el monto del préstamo ajustado para cada código de condado censal. Al igual que con la primera gráfica, puede pasar el cursor sobre ciertos puntos de datos para obtener más información. Seleccione o para producir gráficos para otras variables.
