Métodos y fórmulas para gráficas de dependencia parcial en Ajustar modelo y Descubrir predictores clave con Clasificación TreeNet^®

Supongamos que hay m predictores en un conjunto de datos de entrenamiento, denotados como x₁, x₂, ..., x_m. En primer lugar, ordene los valores distintos del predictor x₁ en el conjunto de datos de entrenamiento en orden creciente. Denote x₁₁ como el primer valor distinto de x₁. A continuación, x₁₁ es la coordenada x para el punto más a la izquierda de la gráfica.

La coordenada y en x₁ = x₁₁ es igual a

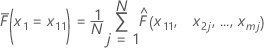
Término	Description
N	el número total de filas en el conjunto de datos de entrenamiento
	los valores observados para en el conjunto de datos de entrenamiento
j	cada fila individual de las filas J
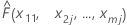	el valor ajustado del modelo cuando x1 = x11, x2 = x2j,...., xm = xmj

Al reemplazar de x₁₁ por cada uno de los valores distintos de x_1,obtenemos las coordenadas y para el resto de los puntos en la gráfica. Los cálculos para el resto de los predictores se realizan de forma similar.

Los cálculos de todas las coordenadas y para todos los valores distintos de x pueden requerir mucho tiempo con grandes conjuntos de datos. Para TreeNet^®, hay una manera más rápida de realizar los cálculos. Referencia a Friedman, J. H. (2001). Greedy function approximation: A gradient boosting machine. The Annals of Statistics, 29(5), page 1221.

Los cálculos para el caso de respuesta multinomial son similares. Aquí el valor ajustado es del modelo para cada clase individual.

Supongamos que hay m predictores en un conjunto de datos de entrenamiento, denotados como x₁, x₂, ..., x_m. En primer lugar, ordene los valores distintos de los predictores x₁, x₂ en el conjunto de datos de entrenamiento en orden creciente. Denote x₁₁, x₂₁ como uno de los pares distintos. A continuación, cada par forma las coordenadas X y Y para un punto en la gráfica de superficie.

La coordenada z en x₁ = x₁₁, x₂ = x₂₁ es igual a

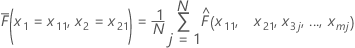
Término	Description
N	el número total de filas en el conjunto de datos de entrenamiento que comparten la similitud de x1 = x11, x2 = x21
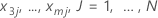	los valores observados para en el conjunto de datos de entrenamiento
j	cada fila individual de las filas J
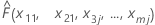	el valor ajustado del modelo cuando x1 = x11, x2 = x21, x3 = x3j...., xm = xmj

La realización de los cálculos para todas las combinaciones de valores distintos de x₁ y x₂ produce todas las coordenadas z para la gráfica de contorno o superficie. Para conjuntos de datos grandes, los cálculos para todos los pares distintos de X y Y requieren mucho tiempo. Para los modelos TreeNet^®, hay una forma más rápida de realizar los cálculos. Referencia a Friedman, J. H. (2001). Greedy function approximation: A gradient boosting machine. The Annals of Statistics, 29(5), page 1221.