Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
Un equipo de investigadores recopila datos de la venta de propiedades residenciales individuales en Ames, Iowa. Los investigadores quieren identificar las variables que afectan el precio de venta. Las variables incluyen el tamaño del lote y varias características de la propiedad residencial.
Después de la exploración inicial para Regresión CART® identificar los predictores importantes, el equipo utiliza Regresión Random Forests® para crear un modelo más intensivo a partir del mismo conjunto de datos. El equipo compara la tabla de resumen del modelo y la gráfica R2 de los resultados para evaluar qué modelo proporciona un mejor resultado de predicción.
Estos datos se adaptaron en base a un conjunto de datos públicos que contenían información sobre los datos de vivienda de Ames. Datos originales de DeCock, Universidad Estatal de Truman.
- Abra los datos de ejemplo Ames_vivienda.MWX.
- Elija .
- En Respuesta, ingrese “Precio de venta”.
- En Predictores continuos, escriba ‘fachada de lote' – ‘año vendido’.
- En Predictores categóricos, escriba ‘tipo' – ‘estado de venta’.
- Haga clic en Opciones.
- En Número de predictores para la división de nodo, elija K por ciento del número total de predictores; K = y escriba 30. Los investigadores quieren usar más que el número predeterminado de predictores para este análisis.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
Método
| Validación del modelo | Validación con datos de "out-of-bag" |
|---|---|
| Número de muestras de bootstrap | 300 |
| Tamaño de la muestra | Igual que el tamaño de los datos de entrenamiento de 2930 |
| Número de predictores seleccionados para la división de nodos | 30% del número total de predictores = 23 |
| Tamaño mínimo del nodo interno | 5 |
| Filas utilizadas | 2930 |
Información de respuesta
| Media | Desv.Est. | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 180796 | 79886.7 | 12789 | 129500 | 160000 | 213500 | 755000 |
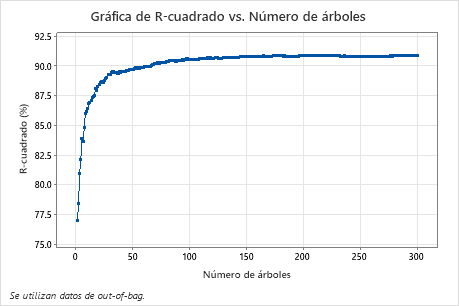
La gráfica de R-cuadrada vs. número de árboles muestra la curva completa del número de árboles creados. El valor de R2 aumenta rápidamente a medida que aumenta el número de árboles y luego se aplana en aproximadamente un 91%.
Resumen del modelo
| Total de predictores | 77 |
|---|---|
| Predictores importantes | 68 |
| Estadísticas | Out-of-Bag |
|---|---|
| R-cuadrado | 90.90% |
| Raíz de los cuadrados medios del error (RMSE) | 24097.3281 |
| Cuadrado medio del error (MSE) | 5.80681E+08 |
| Desviación absoluta media (MAD) | 14746.8323 |
| Media del error porcentual absoluto (MAPE) | 0.0895 |
La tabla resumen del modelo muestra que los valores de R2 han mejorado ligeramente con respecto a los valores de R2 del análisis CART® correspondiente.

La gráfica Importancia relativa de las variables presenta los predictores en el orden de su efecto en la mejora del modelo cuando se realizan divisiones en un predictor sobre la secuencia de árboles. La variable predictora más importante para predecir el precio de venta es la calidad. Si la importancia de la variable predictora superior, Calidad, es del 100%, entonces la siguiente variable importante, Zona de estar, tiene una contribución del 88,8%. Esto significa que los pies cuadrados de la vida son 88.8% tan importantes como la calidad general de la propiedad. La siguiente variable más importante es Vecindario que tiene una contribución del 52.6%.
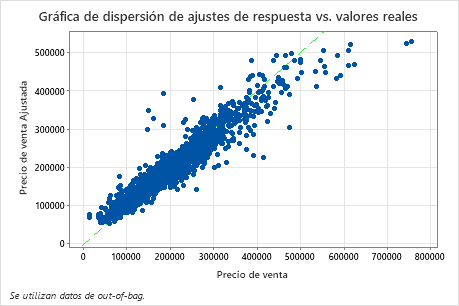
El diagrama de dispersión del precio de venta ajustado frente al precio de venta real muestra la relación entre los valores ajustados y reales para los datos OOB. Puede pasar el cursor sobre los puntos de la gráfica para ver más fácilmente los valores graficados. En este ejemplo, muchos puntos caen aproximadamente cerca de la línea de referencia de y = x, pero varios puntos pueden necesitar investigación para ver discrepancias entre los valores ajustados y reales.
