Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga doble clic aquí para obtener información sobre cómo activar el módulo.
Variables importantes
Minitab Statistical Software ofrece dos métodos para clasificar la importancia de las variables.
Permutación
- A = 87
- B = 9
- C = 4
A continuación, el margen de esa fila es 0.87 - 0.09 = 0.78.
El margen promedio out-of-bag es el margen promedio para todas las filas de datos.
Para determinar la importancia de la variable, permute aleatoriamente los
valores de una variable,
xm a través de los datos out-of-bag. Deje iguales los
valores de respuesta y los demás valores predictores. A continuación, siga los
mismos pasos para calcular el margen promedio de los datos permutados,
.
La importancia para la variable xm proviene de la diferencia de los dos promedios:
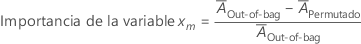
donde 
es el margen promedio antes de la permutación. Minitab redondea los valores
menores que 10–7 a 0.
Gini
Cualquier árbol de clasificación es una colección de divisiones. Cada división proporciona una mejora al árbol.
La siguiente fórmula proporciona la mejora en un nodo individual:
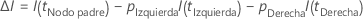
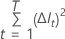
donde 
es el
número de nodos que se dividen y 
para
cualquier nodo 
donde la
variable de interés no es el divisor.
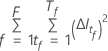
Donde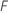 
es el
número de árboles del bosque y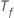 
es el número de nodos que se dividen en el árbol 
.
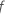El cálculo de la impureza del nodo es similar al método Gini. Para obtener más información sobre el método Gini, vaya a Método de división de nodos: Clasificación CART®.
Log-verosimilitud promedio
Datos out-of-bag
El cálculo utiliza las muestras out-of-bag de cada árbol del bosque. Debido a la naturaleza de las muestras out-of-bag, espere utilizar diferentes combinaciones de árboles para encontrar la contribución a la log-verosimilitud para cada fila de los datos.
Para un árbol determinado en el bosque, un voto de clase para una fila de los datos out-of-bag es la clase pronosticada para la fila del árbol individual. La clase pronosticada para una fila de los datos out-of-bag es la clase con el voto más alto en todos los árboles del bosque. La probabilidad de clase pronosticada para una fila de los datos out-of-bag es la relación entre el número de votos de la clase y el total de votos para la fila. Los cálculos de verosimilitud se derivan de estas probabilidades:
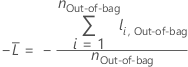
donde
y 
es la probabilidad del evento calculada para la fila
i en los datos out-of-bag.
Notación para los datos out-of-bag
| Término | Description |
|---|---|
| nOut-of-bag | número de filas que están out-of-bag al menos una vez |
| yi, Out-of-bag | valor de respuesta binaria del caso i en los datos out-of-bag. yi, Out-of-bag = 1 para la clase de evento, y 0 en caso contrario. |
Conjunto de prueba
Para un árbol determinado en el bosque, un voto de clase para una fila del conjunto de prueba es la clase pronosticada para la fila del árbol individual. La clase pronosticada para una fila del conjunto de prueba es la clase con el voto más alto en todos los árboles del bosque. La probabilidad de clase pronosticada para una fila del conjunto de prueba es la relación entre el número de votos de la clase y el total de votos para la fila. Los cálculos de verosimilitud se derivan de estas probabilidades:
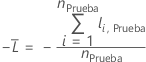
donde
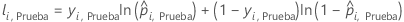
Notación para el conjunto de prueba
| Término | Description |
|---|---|
| nPrueba | tamaño de la muestra del conjunto de prueba |
| yi, Prueba | valor de respuesta binaria del caso i en el conjunto de prueba. yi, k = 1 para la clase de evento, y 0 en caso contrario. |
 | probabilidad del evento pronosticada para el caso i en el conjunto de prueba |
Área bajo la curva ROC
Fórmula
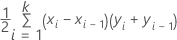
donde k es el número de probabilidades del evento distintas y (x0, y0) es el punto (0, 0).
Para calcular el área de una curva a partir de datos out-of-bag o de un conjunto de prueba, utilice los puntos de la curva correspondiente.
Notación
| Término | Description |
|---|---|
| TPR | tasa de verdaderos positivos |
| FPR | tasa de falsos positivos |
| TP | verdadero positivo, eventos que fueron evaluados correctamente |
| FN | falso negativo, eventos que se evaluaron incorrectamente |
| P | número de eventos positivos reales |
| FP | falso positivo, no eventos que se evaluaron incorrectamente |
| N | número de eventos negativos reales |
| FNR | tasa de falsos negativos |
| TNR | tasa de verdaderos negativos |
Ejemplo
| x (tasa de falsos positivos) | y (tasa de verdaderos positivos) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
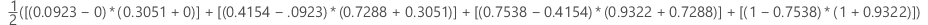
IC del 95% para el área bajo la curva ROC
El siguiente intervalo proporciona los límites superior e inferior para el intervalo de confianza:
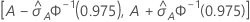
El cálculo del error estándar del área bajo la curva ROC (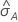
)
proviene de Salford Predictive Modeler®. Para obtener información
general sobre la estimación de la varianza del área bajo la curva ROC, véase
las siguientes referencias:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. y Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G. y Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
Notación
| Término | Description |
|---|---|
| A | área bajo la curva ROC |
 | 0.975 percentil de la distribución normal estándar |
Elevación
Para ver los cálculos generales de la elevación acumulada, vaya a Métodos y fórmulas para la gráfica de elevación acumulada para Clasificación Random Forests®.
Tasa de clasificación errónea
La siguiente ecuación proporciona la tasa de clasificación errónea:
El conteo de clasificaciones erróneas es el número de filas en los datos out-of-bag donde sus clases pronosticadas son diferentes a sus clases verdaderas. El conteo total es el número total de filas en los datos out-of-bag.
Para la validación con un conjunto de datos de prueba, el conteo de clasificaciones erróneas es la suma de clasificaciones erróneas en el conjunto de prueba. El conteo total es el número de filas en el conjunto de datos de prueba.
