En este tema
Paso 1: Determinar qué tan bien se ajusta el modelo a los datos
- R-cuadrado de prueba
- Cuanto mayor sea el valor de R2, mejor se ajusta el modelo a los datos. R2 siempre se encuentra entre 0% y 100%. Los valores atípicos tienen mayor efecto en R2 que en MAD.
- Error cuadrático medio de la raíz de prueba (RMSE)
- Los valores más pequeños indican un mejor ajuste. Los valores atípicos tienen mayor efecto en RMSE que en MAD.
- Error cuadrático medio de prueba (MSE)
- Valores más pequeños indican un mejor ajuste. Los valores atípicos tienen mayor efecto en MSE que en MAD.
- Desviación media absoluta (MAD) de la prueba
- Valores más pequeños indican un mejor ajuste. La desviación absoluta media (MAD) expresa la exactitud en las mismas unidades que los datos, lo que ayuda a conceptualizar la cantidad de error. Los valores atípicos tienen menos efecto en la MAD que en el R2, la RMSE y el MSE.
Resumen del modelo
| Total de predictores | 77 |
|---|---|
| Predictores importantes | 10 |
| Número máximo de funciones base | 30 |
| Número óptimo de funciones base | 13 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| R-cuadrado | 89.61% | 87.61% |
| Raíz de los cuadrados medios del error (RMSE) | 25836.5197 | 27855.6550 |
| Cuadrado medio del error (MSE) | 667525749.7185 | 775937512.8264 |
| Desviación absoluta media (MAD) | 17506.0038 | 17783.5549 |
Resultados clave: Prueba R-cuadrado, Error cuadrático medio de la raíz de prueba (RMSE), Error cuadrático medio de prueba (MSE), Desviación absoluta media de prueba (MAD)
En estos resultados, la prueba R-cuadrado es de aproximadamente 88%. El error cuadrático medio de la raíz de prueba es de aproximadamente 27,856. El error cuadrático medio de la prueba es de aproximadamente 775,937,513. La desviación absoluta media de la prueba es de aproximadamente 17,784.
Paso 2: Determinar qué variables son más importantes para el modelo
Utilice el gráfico de importancia relativa de variables para ver qué predictores son las variables más importantes para el modelo.
Las variables importantes están en al menos 1 función base en el modelo. La variable con la puntuación de mejora más alta se establece como la variable más importante y las otras variables se clasifican en consecuencia. La Importancia relativa de las variables estandariza los valores de importancia para facilitar la interpretación. La importancia relativa se define como la mejora porcentual con respecto al predictor más importante.
Los valores de importancia relativa de las variables oscilan entre el 0% y el 100%. La variable más importante siempre tiene una importancia relativa del 100%. Si una variable no está en una función base, esa variable no es importante.
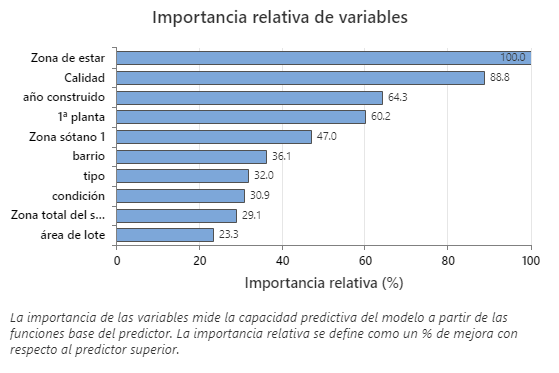
Resultado clave: Importancia relativa de variables
- Calidad es aproximadamente un 89% tan importante como Zona de estar.
- año construido es aproximadamente un 64% tan importante como Zona de estar.
- 1ª planta es aproximadamente un 60% tan importante como Zona de estar.
Aunque estos resultados incluyen 10 variables con importancia positiva, las clasificaciones relativas proporcionan información sobre cuántas variables controlar o supervisar para una determinada aplicación. Las caídas pronunciadas en los valores de importancia relativa de una variable a la siguiente variable pueden guiar las decisiones sobre qué variables controlar o supervisar. Por ejemplo, en estos datos, las 2 variables más importantes tienen valores de importancia que están relativamente cerca entre sí antes de una caída de más del 20% en importancia relativa a la siguiente variable. Del mismo modo, 2 variables tienen valores de importancia similares superiores al 60%. Puede quitar variables de diferentes grupos y rehacer el análisis para evaluar cómo afectan las variables de varios grupos a los valores de exactitud de predicción de la tabla de resumen del modelo.
Paso 3: Explore los efectos de los predictores
Utilice las gráficas de dependencia parcial, las funciones base y los coeficientes de la ecuación de regresión para determinar el efecto de los predictores. Los efectos de los predictores explican la relación entre los predictores y la respuesta. Considere todas las funciones básicas de un predictor para comprender el efecto del predictor en la variable de respuesta.
Además, considere el uso de los predictores importantes y las formas de sus relaciones cuando construya otros modelos. Por ejemplo, si el modelo de regresión MARS® incluye interacciones, considere si incluir esas interacciones en un modelo de regresión de mínimos cuadrados para comparar el rendimiento de los dos tipos de modelos. En las aplicaciones en las que se controlan los predictores, los efectos proporcionan una forma natural de optimizar la configuración para lograr un objetivo para la variable de respuesta.
En un modelo aditivo, los gráficos de dependencia parcial de un predictor muestran cómo los predictores continuos importantes afectan la respuesta prevista. La gráfica de dependencia parcial para un predictor indica cómo se espera que cambie la respuesta con los cambios en los niveles del predictor. Para MARS®, los valores de la gráfica provienen de las funciones base para el predictor en el eje x. La contribución en el eje y está estandarizada para que el valor mínimo en la parcela sea 0.
Resultado clave: Gráfica de dependencia parcial
Este gráfico ilustra que aumenta a medida que Precio de venta aumenta Zona de estar de los pies cuadrados mínimos en el conjunto de datos a aproximadamente 3,000 pies cuadrados. Después de Zona de estar alcanzar los 3,000 pies cuadrados, la contribución se vuelve plana en Precio de venta aproximadamente $ 152,000.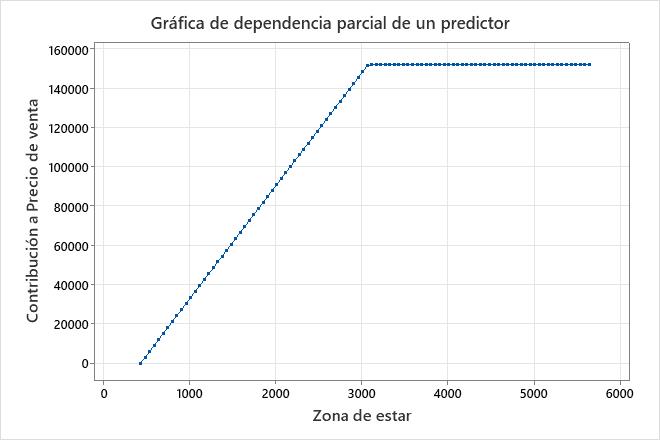
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Resultado clave: Ecuación de regresión
En estos resultados, BF2 tiene un coeficiente negativo en la ecuación de regresión. El coeficiente para la función base es −57.6167. La disposición de la función base es máx.(0, c − X). En esta disposición, el valor de la función base disminuye cuando aumenta el predictor. La combinación de esta disposición y el coeficiente negativo crea una relación positiva entre la variable predictora y la variable de respuesta. La pendiente de es 57.6167 de Zona de estar 438 a 3,078.
Para obtener más ejemplos de funciones de base comunes, vaya a Ecuación de regresión para MARS®.
