Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
y = b0 + b 1 BF1+ b 2 BF2 + ... + b kBFk
- y es la variable de respuesta
- b0 es el término constante
- b1 + b2 + ... + bk son coeficientes para las funciones base
- BF1 + BF2 + ... + BFk son las funciones básicas
Resuelve las funciones base para los valores del predictor para calcular el valor previsto de la respuesta.
Funciones básicas
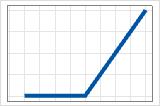
- máx.(0, X − c)
- Coeficiente positivo
- La contribución es 0 hasta c, luego aumenta.
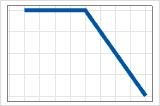
- máx.(0, X − c)
- Coeficiente negativo
- La contribución es la máxima hasta c, luego disminuye.
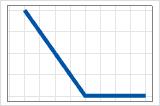
- máx.(0, c − X)
- Coeficiente positivo
- La contribución comienza en el máximo y disminuye hasta c. Después de c, la contribución es 0.
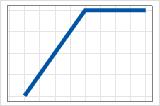
- máx.(0, c − X)
- Coeficiente negativo
- La contribución comienza en 0 y aumenta hasta c. Después de c, las contribuciones están en el valor máximo.
Si c es igual al valor mínimo o máximo del predictor, entonces el predictor tiene el mismo efecto para todos los valores de la función base. La gráfica de dependencia parcial para estos 2 casos muestra una línea recta. MARS® hace de c uno de los puntos finales en un análisis que no permite transformaciones para el predictor.
Para los predictores categóricos, las funciones base son funciones indicadoras. La función tiene un valor de 0 para algunas categorías y un valor de 1 para las otras categorías. Las funciones básicas tienen la siguiente forma:
Cuando X es x1, ... xk donde k es el número de niveles en la función base, k ≥ 1.
El valor de la función es 1 para las categorías de la función base. La multiplicación de la función base por el coeficiente en la ecuación de regresión determina el efecto cuando la función cambia de 0 a 1.
Ejemplo de un predictor continuo en 1 función base
En estos resultados, BF2 tiene un coeficiente negativo en la ecuación de regresión. El coeficiente para la función base es −57.6167. La disposición de la función base es máx.(0, c − X). En esta disposición, el valor de la función base disminuye cuando aumenta el predictor. La combinación de esta disposición y el coeficiente negativo crea una relación positiva entre la variable predictora y la variable de respuesta. El efecto de Zona de estar es aumentar Precio de venta en la región de 438 a 3,078. La pendiente de es 57.6167 de Zona de estar 438 a 3,078.
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Una gráfica predictora de dependencia parcial
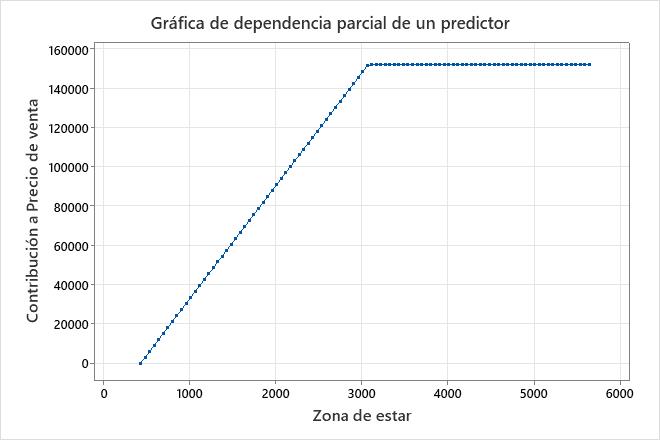
En un modelo aditivo, utilice los gráficos de dependencia parcial de un predictor para obtener información sobre cómo los predictores continuos importantes afectan la respuesta prevista. La gráfica de dependencia parcial para un predictor indica cómo se espera que cambie la respuesta con los cambios en los niveles del predictor. Para MARS®, los valores de la gráfica provienen de las funciones base para el predictor en el eje x. La contribución en el eje y está estandarizada para que el valor mínimo en la parcela sea 0.
Este gráfico ilustra que aumenta a medida que Precio de venta aumenta Zona de estar de los pies cuadrados mínimos en el conjunto de datos a aproximadamente 3,000 pies cuadrados. Después de Zona de estar alcanzar los 3,000 pies cuadrados, la contribución se vuelve plana en Precio de venta aproximadamente $ 152,000.
Ejemplo de un predictor categórico en 1 función base
En estos resultados, BF3 es para el predictor Calidad. La función base es para cuando el valor de Calidad es 8, 9 o 10. El coeficiente para BF3 en la ecuación es 115.438. Esta función básica indica que cuando el valor de la calidad cambia de un valor de 1 a 7 a un valor de 8, 9 o 10, el precio de venta aumenta en $115,438 en el modelo. Calidad también está en BF11 y BF25. Para comprender el efecto del predictor en la variable de respuesta, considere todas las funciones base.
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Nota
En una ecuación de regresión tradicional, el coeficiente en la ecuación de regresión siempre representa el cambio de 0 a 1. En MARS®, el coeficiente puede representar el cambio de 1 a 0. Considere una variable categórica binaria que es 0 cuando un paciente informa que no tiene dolor de cabeza y 1 cuando un paciente informa que tiene dolor de cabeza. Supongamos que el predictor tiene la siguiente función base:
- BF1 = cuando el dolor de cabeza es 0
Múltiples funciones básicas para 1 predictor
MARS® Utiliza múltiples funciones básicas para un solo predictor para modelar relaciones no lineales más complejas entre un predictor y la respuesta. Las funciones de base adicionales crean cambios adicionales en la pendiente de la relación entre el predictor y la variable de respuesta. MARS® Permite predictores en múltiples funciones de base en modelos aditivos.
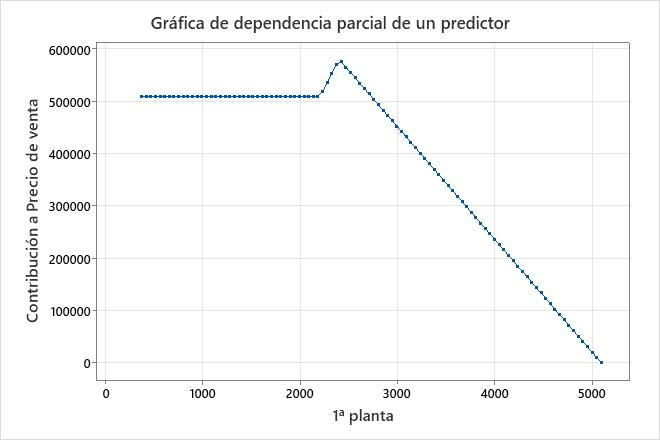
En estos resultados, BF21 es para el predictor 1ª planta. La función base BF27 también es para 1ª planta. BF21 y BF27 tienen la misma disposición, máx.(0, X − c). Las funciones de base en esta disposición afectan a la variable de respuesta cuando el predictor tiene un valor mayor que c. Para 2 funciones base con esta disposición, ninguna función base afecta la respuesta hasta que el predictor alcanza el valor mínimo en 1 de las funciones base. En estos resultados, ese valor es 2,207 en BF27. 1ª planta tiene una pendiente de 0 desde el valor mínimo hasta 2,207. Después de 2,207, se aplica la pendiente de BF27, lo que resulta en una pendiente de 361.254. Esta pendiente persiste hasta que el predictor alcanza la constante en BF21, momento en el que los coeficientes de BF27 y BF21 afectan . Precio de venta La suma de los dos coeficientes da la nueva pendiente, 361.254 + (−576.789) = −215.535. En un modelo aditivo, MARS® muestra una gráfica de dependencia parcial de un predictor para mostrar el efecto del predictor.
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Funciones básicas para valores faltantes
En la búsqueda de las funciones base, MARS® crea variables indicadoras para cualquier predictor con valores faltantes. La variable indicadora muestra si falta un valor del predictor. Si el análisis incluye una función base para un predictor con valores faltantes en el modelo, entonces el modelo también incluye una función base para la variable indicadora. Las otras funciones base para el predictor interactúan con la función base para la variable indicadora.
Cuando a un predictor le falta un valor, la función base de la variable indicadora anula las otras funciones base de ese predictor mediante la multiplicación por 0. Estas funciones básicas para valores faltantes se encuentran en todos los modelos donde faltan valores importantes predictores, incluso modelos aditivos y modelos que deshabilitan otros tipos de transformaciones.
En estos resultados, BF7 es para el predictor Zona sótano 1. BF 7 tiene un valor de 1 cuando Zona sótano 1 está en los datos. BF 7 tiene un valor de 0 cuando Zona sótano 1 falta. BF7 no está presente en la ecuación de regresión porque la función base no era importante en el modelo final, pero BF7 interactúa con BF10. BF10 es importante y está presente en la ecuación de regresión. El efecto de BF7 es multiplicar BF10 por 0 cuando falta, lo que elimina el efecto cuando Zona sótano 1Zona sótano 1 falta.
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Funciones básicas para interacciones
Para modelar interacciones, MARS® multiplica las funciones básicas para diferentes predictores. MARS® no considera las interacciones en el modelo aditivo predeterminado. Las gráficas de dependencia parcial no están disponibles para un análisis que considere las interacciones.
Una interacción significa que el efecto de un predictor depende del valor de otros predictores. Por ejemplo, la velocidad a la que el grano se seca en un horno depende del tiempo en el horno, pero el efecto del tiempo depende de la temperatura del horno. Las variables de tiempo y temperatura interactúan.
En los resultados para un modelo con interacciones, BF9 es para el predictor Calidad. BF12 es para el predictor 1ª planta. El cálculo de BF12 incluye la multiplicación por BF9, por lo que los dos predictores interactúan. La determinación del efecto de Calidad o 1ª planta requiere el conocimiento del valor del otro predictor. El coeficiente para BF12 de −63.1685 se aplica solo cuando el valor de BF9 es 1. El valor de BF9 es 1 cuando Calidad es 8, 9 o 10. Debido a la disposición de BF12, 1ª planta tiene una pendiente de 63.1685 cuando los pies cuadrados son menores que 2,470 y el valor de Calidad es 8, 9 o 10.
Ecuación de regresión
BF4 = máx.(0, 2002 - año construido)
BF5 = cuando Zona sótano 1 no es un valor faltante
BF7 = máx.(0, Zona sótano 1 - 1758) * BF5
BF8 = máx.(0, 1758 - Zona sótano 1) * BF5
BF9 = cuando Calidad es 8, 9, 10
BF12 = máx.(0, 2470 - 1ª planta) * BF9
BF14 = cuando Calidad es 7, 9, 10
BF15 = cuando tipo es 75, 90, 150, 160, 180, 190
BF19 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker, Verdes * BF5
BF21 = cuando condición es 1, 2, 3, 4, 5, 6 * BF4
BF25 = máx.(0, 1ª planta - 372) * BF7
BF26 = cuando Zona total del sótano no es un valor faltante * BF14
BF28 = máx.(0, Zona total del sótano - 689) * BF26
Precio de venta = 320349 - 66.4387 * BF2 - 28.2065 * BF8 + 123645 * BF9 - 63.1685 * BF12 -
23751.7 * BF15 + 22818.2 * BF19 - 523.924 * BF21 - 0.036887 * BF25 + 53.9878 * BF28
