Nota
Este comando está disponible con el Módulo de análisis predictivo. Haga clic aquí para obtener más información sobre cómo activar el módulo.
Un equipo de investigadores recopila datos de la venta de propiedades residenciales individuales en Ames, Iowa. Los investigadores quieren identificar las variables que afectan el precio de venta. Las variables incluyen el tamaño del lote y varias características de la propiedad residencial. Los investigadores quieren evaluar qué tan bien el mejor modelo MARS® se ajusta a los datos.
- Abra los datos de muestra, Ames_vivienda.MWX.
- Seleccione .
- En Respuesta, ingrese “Precio de venta”.
- En Predictores continuos, escriba ‘fachada de lote' – ‘año vendido’.
- En Predictores categóricos, escriba tipo – ‘estado de venta’.
- Haga clic en Aceptar.
Interpretar los resultados
Por defecto, Regresión MARS® se ajusta a un modelo aditivo para que todas las funciones de base en la ecuación de regresión usen 1 predictor. El primer predictor de la lista es BF2. BF2 utiliza el predictor Zona de estar. Debido a que el predictor está en 1 función base, el predictor tiene 2 pendientes diferentes en el modelo. La función máx.(0, 3078 - Zona de estar) define que la pendiente es distinta de cero cuando la superficie habitable es inferior a 3.078.
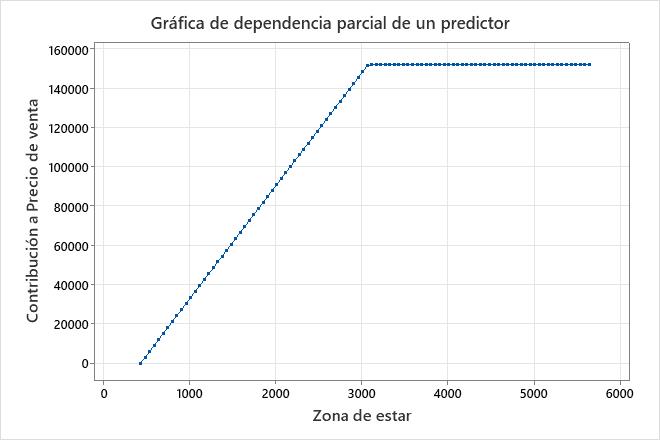
Los resultados para un modelo aditivo incluyen gráficas de dependencia parcial para predictores continuos que son importantes en el modelo. Utilice la gráfica para ver el efecto de todas las funciones base de un predictor en todo el rango del predictor. En estos resultados, la gráfica de dependencia parcial muestra que para un valor de Zona de estar 438 a 3.078, la pendiente es de aproximadamente 57,6. Cuando Zona de estar es mayor que 3.078, la pendiente es 0.
En estos resultados, BF2 tiene un coeficiente negativo en la ecuación de regresión. La disposición de la función base es máx.(0, c- X). En esta disposición, el valor de la función base disminuye cuando aumenta el predictor. La combinación de esta disposición y el coeficiente negativo crea una relación positiva entre la variable predictora y la variable de respuesta. El efecto de Zona de estar es aumentar Precio de venta en la región de 438 a 3,078.
El análisis también incluye predictores categóricos. Por ejemplo, BF3 es para el predictor Calidad. La función base es para cuando el valor de Calidad es 8, 9 o 10. El coeficiente para BF3 en la ecuación es 115.438. Esta función básica indica que cuando el valor de la calidad cambia de un valor de 1 a 7 a un valor de 8, 9 o 10, el precio de venta aumenta en $115,438 en el modelo. Calidad también está en BF11 y BF25. Para comprender el efecto del predictor en la variable de respuesta, considere todas las funciones base.
Dos de los predictores que son importantes en el modelo tienen valores faltantes en los datos de entrenamiento: Zona sótano 1 y Zona total del sótano. La lista de funciones base incluye funciones base que identifican cuándo faltan estos predictores: BF7 y BF17. Cuando cualquiera de los dos un predictor le falta un valor, la función base de la variable indicadora anula las otras funciones base de ese predictor mediante la multiplicación por 0.
Ecuación de regresión
BF3 = cuando Calidad es 8, 9, 10
BF6 = máx.(0, 2002 - año construido)
BF7 = cuando Zona sótano 1 no es un valor faltante
BF10 = máx.(0, 1696 - Zona sótano 1) * BF7
BF11 = cuando Calidad es 1, 8
BF13 = cuando tipo es 90, 150, 160, 180, 190
BF15 = cuando barrio es Alturas de Northridge, Arroyo despejado, Bluestem, Colinas Verdes,
Crawford, Muy bien, Northridge, Pueblos somerset, Puente de piedra, Timberland, Veenker
BF17 = cuando Zona total del sótano no es un valor faltante
BF19 = máx.(0, Zona total del sótano - 1392) * BF17
BF21 = máx.(0, 1ª planta - 2402)
BF23 = cuando condición es 1, 2, 3, 4, 5, 6
BF25 = cuando Calidad es 1, 7, 10
BF27 = máx.(0, 1ª planta - 2207)
BF30 = máx.(0, 15138 - área de lote)
Precio de venta = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 -
66735.2 * BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2
* BF23 + 22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
Nota
En estos resultados, la lista de funciones básicas tiene 15 funciones básicas, pero el número óptimo de funciones básicas es 13. La ecuación de regresión contiene 13 funciones básicas. La lista de funciones base contiene BF7 y BF17, que son las funciones base que identifican los valores que faltan. Estas funciones de base no son importantes por sí solas porque no redujeron el MSE tanto como otras funciones básicas en la búsqueda. Estas 2 funciones básicas están en la lista para mostrar el cálculo completo de BF10 y BF 19, que son importantes.
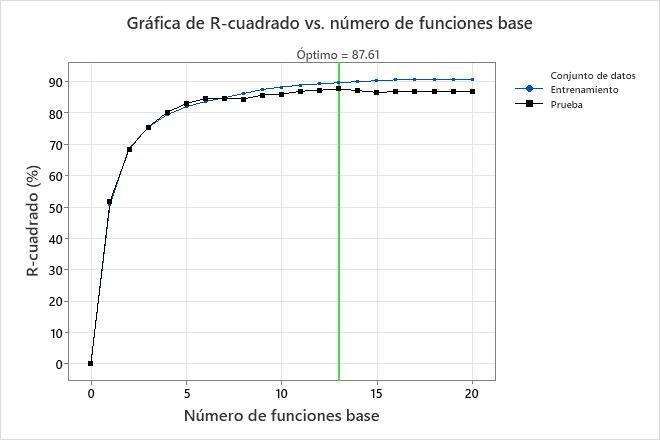
El gráfico R-cuadrado vs Número de funciones base muestra el resultado de la eliminación hacia atrás para encontrar el número óptimo de funciones base. Para utilizar un modelo con un número diferente de funciones básicas, seleccione Seleccionar modelo alternativo. Por ejemplo, si un modelo con muchas menos funciones base es casi tan preciso como el modelo óptimo, considere si usar el modelo más simple. En estos resultados, los valores de R-cuadrado para los conjuntos de datos de entrenamiento y prueba son los mismos para el modelo con 7 funciones básicas. Este modelo más pequeño es de interés si el sobreajuste es una preocupación.
Resumen del modelo
| Total de predictores | 77 |
|---|---|
| Predictores importantes | 10 |
| Número máximo de funciones base | 30 |
| Número óptimo de funciones base | 13 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| R-cuadrado | 89.61% | 87.61% |
| Raíz de los cuadrados medios del error (RMSE) | 25836.5197 | 27855.6550 |
| Cuadrado medio del error (MSE) | 667525749.7185 | 775937512.8264 |
| Desviación absoluta media (MAD) | 17506.0038 | 17783.5549 |
La tabla de resumen del modelo incluye medidas del rendimiento del modelo. Puede utilizar estos valores para comparar modelos. Para estos resultados, la prueba R-cuadrado es de aproximadamente 88%.
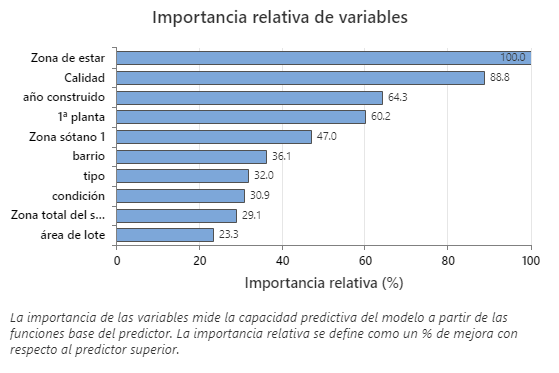
El gráfico de importancia relativa de la variable traza los predictores en orden de su efecto en el modelo. La variable predictora más importante es Zona de estar. Si la contribución de la variable predictora superior, Zona de estar, es del 100%, entonces la siguiente variable importante, Calidad, tiene una contribución del 88.8%. Esta contribución significa que Calidad es un 88,8% tan importante como Zona de estar en este modelo.
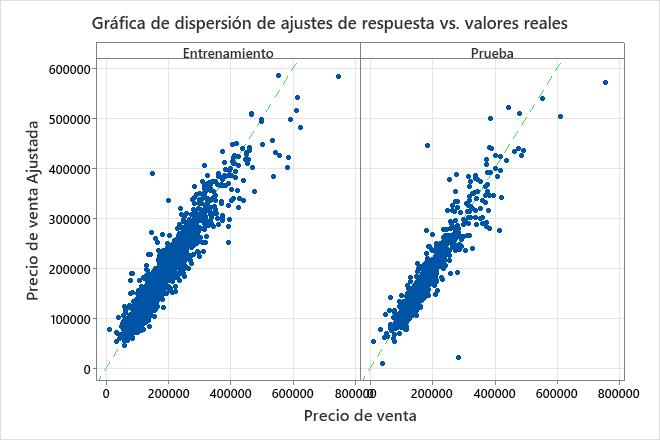
El diagrama de dispersión de los precios de venta ajustados frente a los precios de venta reales muestra la relación entre los valores ajustados y reales tanto para los datos de entrenamiento como para los datos de prueba. Puede pasar el cursor sobre los puntos de la gráfica para ver más fácilmente los valores graficados. En este ejemplo, la mayoría de los puntos caen aproximadamente cerca de la línea de referencia de y=x.
El modelo se ajusta mal a algunos puntos distintos, como el del conjunto de datos de prueba que tiene un precio de venta ajustado de menos de $ 100,000 pero un precio de venta real más cercano a $ 250,000. Considere si investigar este caso para mejorar el ajuste del modelo.
