En este tema
Paso 1: Investigar árboles alternativos
La gráfica de R-cuadrado vs.número de nodos terminales muestra el valor de R2 para cada árbol. Por opción predeterminada, el árbol de regresión inicial es el árbol más pequeño con un valor de R2 dentro de 1 error estándar del valor para el árbol que maximiza el valor de R2. Cuando el análisis utiliza la validación cruzada o un conjunto de datos de prueba, el valor de R2 procede del ejemplo de validación. Los valores de la muestra de validación normalmente se nivelan y, finalmente, comienzan a disminuir a medida que el árbol crece.
Haga clic en Seleccionar árbol alternativo para abrir una gráfica interactiva que incluya una tabla de estadísticas de resumen del modelo. Utilice la gráfica para investigar árboles alternativos con un rendimiento similar.
- El árbol que Minitab selecciona es parte de un patrón donde el criterio mejora. Uno o más árboles que tienen algunos nodos más forman parte del mismo patrón. Normalmente, desea realizar predicciones desde un árbol con la mayor exactitud de predicción posible.
- El árbol que Minitab selecciona es parte de un patrón donde el criterio es relativamente plano. Uno o más árboles con estadísticas de resumen del modelo similares tienen muchos menos nodos que el árbol óptimo. Normalmente, un árbol con menos nodos terminales proporciona una imagen más clara de cómo cada variable predictora afecta a los valores de respuesta. Un árbol más pequeño también facilita la identificación de algunos grupos objetivo para estudios posteriores. Si la diferencia en la exactitud de predicción para un árbol más pequeño es insignificante, también puede utilizar el árbol más pequeño para evaluar las relaciones entre la respuesta y las variables predictoras.
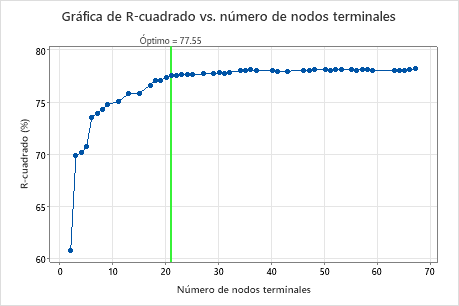
Resultado clave: Gráfica de R-cuadrado vs. Número de nodos terminales para un árbol con 21 nodos terminales
El árbol de regresión con 21 nodos terminales tiene un valor de R2 de aproximadamente 0.78. Este árbol tiene la etiqueta "Óptimo" porque el criterio para la creación del árbol era el árbol más pequeño con un valor de R2 dentro de 1 desviación estándar del valor máximo de R2. Debido a que esta gráfica muestra que los valores de R2 son relativamente estables entre árboles con unos 20 nodos y árboles con unos 70 nodos, los investigadores quieren ver el rendimiento de algunos de los árboles aún más pequeños que son similares al árbol en los resultados. Compare la siguiente gráfica para ver los resultados de un árbol con 17 nodos.
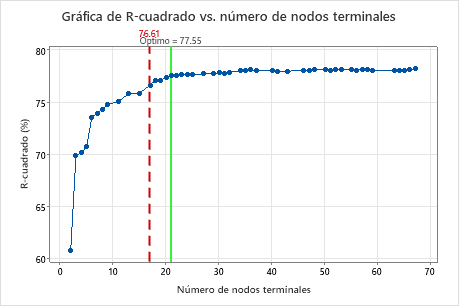
Resultado clave: Gráfica de R-cuadrado vs. Número de nodos terminales para un árbol con 17 nodos terminales
El árbol de regresión con 17 nodos terminales tiene un valor de R2 de 0.7661. El árbol de los resultados iniciales mantiene la etiqueta "Óptimo" cuando se utiliza Seleccionar árbol alternativo para crear resultados para un árbol diferente.
Paso 2: Investigar nodos interesantes en el diagrama de árbol
Después de seleccionar un árbol, investigue los nodos terminales distintivos en el diagrama de árbol. Por ejemplo, es posible que le interesen nodos con medias grandes o con pequeñas desviaciones estándar. En la vista detallada, puede ver la media, la desviación estándar y los conteos totales de cada nodo.
Nota
Haga clic con el botón derecho en el diagrama de árbol para realizar las siguientes interacciones:
- Resaltar los 5 nodos con la menor variación del valor ajustado para el nodo. Estos nodos son los nodos óptimos.
- Resaltar los 5 nodos con las medias o medianas más altas, dependiendo del criterio del árbol.
- Resaltar los 5 nodos con las medias o medianas más bajas, dependiendo del criterio del árbol.
- Copiar los valores de los predictores que conducen a un nodo que seleccione. Estos valores son las reglas del nodo.
- Mostrar la vista de división de nodos. Esta vista es útil cuando tiene un árbol grande y desea ver solo qué variables dividen los nodos.
Los nodos continúan dividiéndose hasta que los nodos terminales no se pueden dividir en agrupaciones adicionales. Explore otros nodos para ver qué variables son más interesantes.
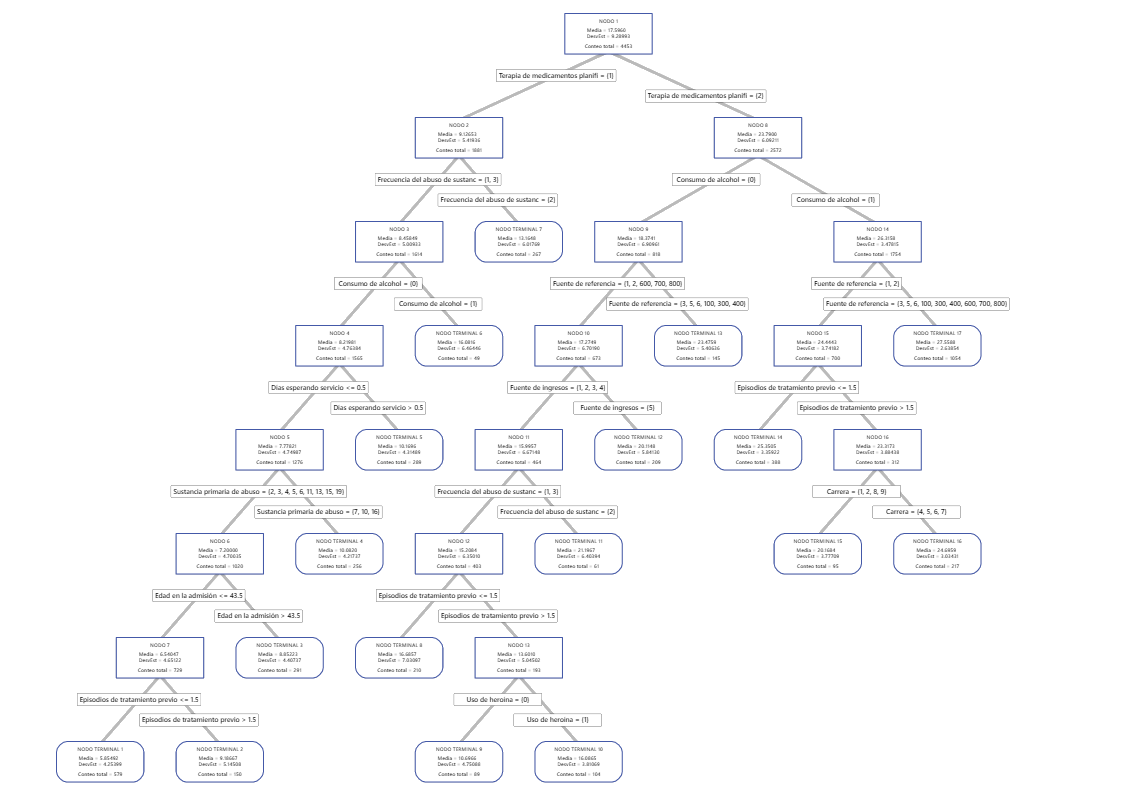
Resultado clave: Diagrama de árbol para árbol con 17 nodos
El diagrama de árbol muestra los 4453 casos del conjunto de datos completo. Puede alternar las vistas del árbol entre la vista detallada y la vista de división de nodos.
- El nodo 2 tiene los casos en donde Terapia de medicamentos planificada = 1. Este nodo tiene 1881 casos. La media del nodo es menor que la media general. La desviación estándar para Nodo 2 es aproximadamente 5.4, que es menor que la desviación estándar general porque una división produce nodos más puros.
- Nodo 8 tiene los casos donde Terapia de medicamentos planificada = 2. Este nodo tiene 2572 casos. La media para el nodo es mayor que la media general. La desviación estándar para Nodo 8 es aproximadamente 6.1, que también es menor que la desviación estándar general.
Entonces, Nodo 2 se divide entre Frecuencia del abuso de sustancias y Nodo 8 se divide entre el Consumo de alcohol. Nodo terminal 17 tiene los casos para Terapia de medicamentos planificada = 2, Consumo de alcohol = 1 y Fuente de referencia = 3, 5, 6, 100, 300, 400, 600, 700 u 800. Los investigadores señalan que Nodo terminal 17 tiene la media más alta, la desviación estándar más pequeña y la mayoría de los casos.
Nodo terminal 1 tiene la media más pequeña y una desviación estándar de aproximadamente 4.3. Debido a que la media de Nodo terminal 1 es aproximadamente 5.9 y los valores de respuesta no pueden ser negativos, las estadísticas del nodo sugieren que los datos en Nodo terminal 1 son probablemente asimétricos hacia la derecha.
Paso 3: Determinar las variables importantes
Utilice el gráfico de importancia relativa de variable para ver qué predictores son las variables más importantes para el árbol.
Las variables importantes son divisores primarios o sustitutos en el árbol. La variable con la puntuación de mejora más alta se establece como la variable más importante, y las otras variables se clasifican en consecuencia. La importancia relativa de las variables estandariza los valores de importancia para facilitar la interpretación. La importancia relativa se define como la mejora porcentual con respecto al predictor más importante.
Los valores de importancia relativa de la variable oscilan entre 0% y 100%. La variable más importante siempre tiene una importancia relativa de 100%. Si una variable no está en el árbol, esa variable no es importante.
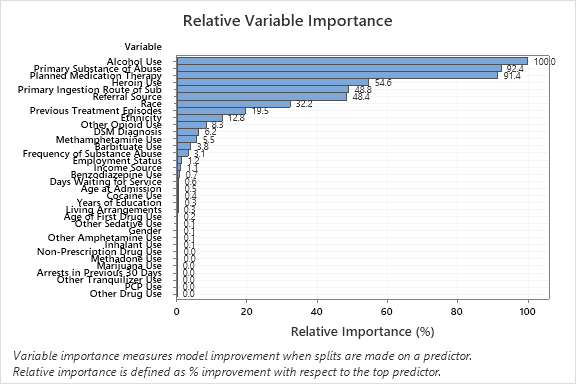
Resultado clave: Importancia relativa de la variable
- Sustancia primaria de abuso y Terapia de medicamentos planificada son aproximadamente 92% tan importantes como Consumo de alcohol.
- Uso de heroína es aproximadamente 55% tan importante como Consumo de alcohol.
- Ruta de Ingestión Primaria de Sub y Fuente de referencia son aproximadamente 48% tan importantes como Consumo de alcohol.
Aunque estos resultados incluyen 33 variables con importancia positiva, las clasificaciones relativas proporcionan información sobre cuántas variables controlar o supervisar para una determinada aplicación. Las caídas pronunciadas en los valores de importancia relativa de una variable a la siguiente variable pueden guiar las decisiones sobre qué variables controlar o supervisar. Por ejemplo, en estos datos, las tres variables más importantes tienen valores de importancia que son relativamente cercanos antes de una caída de casi 40% en importancia relativa para la siguiente variable. Del mismo modo, tres variables tienen valores de importancia similares cercanos a 50%. Puede quitar variables de diferentes grupos y rehacer el análisis para evaluar cómo afectan las variables de varios grupos a los valores de exactitud de predicción de la tabla de resumen del modelo.
