Un proveedor de atención médica maneja un centro que proporciona servicios de tratamiento de abuso de sustancias. Uno de los servicios en el centro es un programa de desintoxicación ambulatoria donde un plan regular de tratamiento puede durar de 1 a 30 días. Un equipo responsable de proyectar personal y suministros quiere estudiar si pueden hacer mejores predicciones sobre el tiempo que un paciente utiliza servicios basándose en información que puede recopilar sobre el paciente cuando el paciente entra en el programa. Estas variables incluyen información demográfica y variables sobre el abuso de sustancias del paciente.
En primer lugar, el equipo considera un análisis de regresión tradicional en Minitab. Debido al patrón de valor faltante en sus datos, el análisis omite más del 70% de los datos. La omisión de un porcentaje tan grande de datos implica que se pierde mucha información. Los resultados analíticos de los casos sin que falten datos pueden ser muy diferentes de los resultados utilizando todo el conjunto de datos. Debido a que Regresión CART® maneja automáticamente los valores faltantes en las variables predictoras, el equipo decide usarlos Regresión CART® para evaluar más a fondo sus datos.
- Abra el conjunto de datos de muestra DuracionDelServicio.MWX.
- Elija .
- En Respuesta, ingrese 'Duración del servicio'.
- En Predictores continuos, ingrese 'Edad en la admisión'-'Años de Educación'.
- En Predictores categóricos, ingrese 'Otro uso estimulante'-'Diagnóstico de DSM'.
- Haga clic en Validación.
- En Método de validación, seleccione Validación cruzada de K pliegues.
- Seleccione Asignar filas de cada pliegue con la columna de ID.
- En Columna ID, ingrese Doblar.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
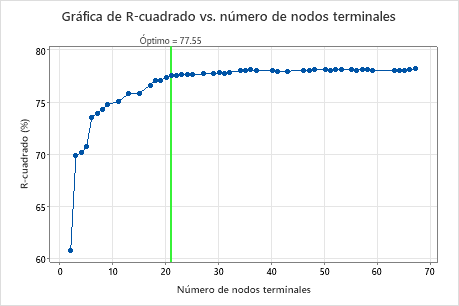
Por opción predeterminada, Minitab muestra el árbol más pequeño que tiene un valor de R2 dentro de 1 error estándar del árbol con el valor de R2 máximo. Debido a que el equipo de atención médica utiliza validación de k pliegues, el criterio es el valor máximo de R2 de k pliegues. Este árbol tiene 21 nodos terminales.
Seleccionar un árbol alternativo
- En la salida, haga clic en Seleccionar árbol alternativo
- En la gráfica, seleccione el árbol de 17 nodos.
- Haga clic en Crear árbol.
Interpretar los resultados
Los investigadores examinan la gráfica de la estadística de R2 de la validación cruzada y el número de nodos terminales. Dado que el árbol con 17 nodos tiene una estadística de R2 cercana a los valores más grandes de la gráfica, los resultados para el resto de la salida son para el árbol con 17 nodos.
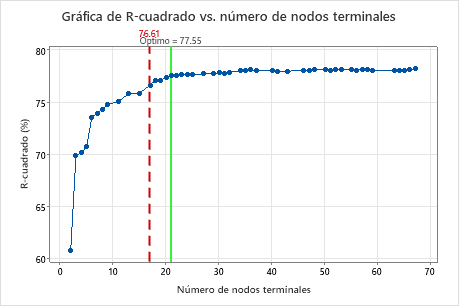
Los investigadores examinan primero el resumen del modelo para evaluar el rendimiento del árbol más pequeño. Los valores de las estadísticas de entrenamiento y prueba son cercanos, por lo que el árbol no parece tener un ajuste excesivo. La estadística de R2 es casi tan alta como el árbol de 21 nodos, por lo que los investigadores deciden utilizar el árbol con 17 nodos para explorar las relaciones entre las variables predictoras y los valores de respuesta.
Método
| División de nodos | Cuadrado mínimo del error |
|---|---|
| Árbol óptimo | Dentro de 2.5 error estándar del R-cuadrado máximo |
| Validación del modelo | Validación cruzada con filas definidas por Doblar |
| Filas utilizadas | 4453 |
Información de respuesta
| Media | Desv.Est. | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 17.5960 | 9.29097 | 1 | 10 | 18 | 26 | 30 |
Resumen del modelo
| Total de predictores | 44 |
|---|---|
| Predictores importantes | 33 |
| Número de nodos terminales | 17 |
| Tamaño mínimo del nodo terminal | 49 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| R-cuadrado | 77.99% | 76.61% |
| Raíz de los cuadrados medios del error (RMSE) | 4.3585 | 4.4932 |
| Cuadrado medio del error (MSE) | 18.9967 | 20.1887 |
| Desviación absoluta media (MAD) | 3.4070 | 3.5226 |
| Media del error porcentual absoluto (MAPE) | 0.6535 | 0.6674 |
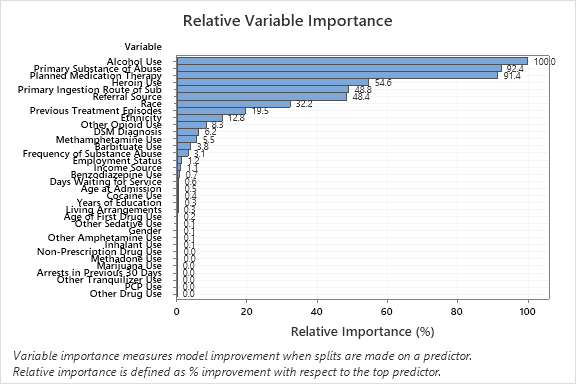
- 'Sustancia primaria de abuso' y 'Terapia de medicamentos planificada' son aproximadamente un 92% tan importantes como 'Consumo de alcohol'.
- 'Uso de heroína' es aproximadamente un 55% tan importante como 'Consumo de alcohol'.
- 'Ruta de Ingestión Primaria de Sub' y 'Fuente de referencia' son aproximadamente un 48% tan importantes como 'Consumo de alcohol'.
Aunque estos resultados incluyen 33 variables con importancia positiva, las clasificaciones relativas proporcionan información sobre cuántas variables controlar o supervisar para una determinada aplicación. Las caídas pronunciadas en los valores de importancia relativa de una variable a la siguiente variable pueden guiar las decisiones sobre qué variables controlar o supervisar. Por ejemplo, en estos datos, las tres variables más importantes tienen valores de importancia que son relativamente cercanos antes de una caída de casi 40% en importancia relativa para la siguiente variable. Del mismo modo, tres variables tienen valores de importancia similares cercanos al 50%. Puede quitar variables de diferentes grupos y rehacer el análisis para evaluar cómo afectan las variables de varios grupos a los valores de exactitud de predicción de la tabla de resumen del modelo.
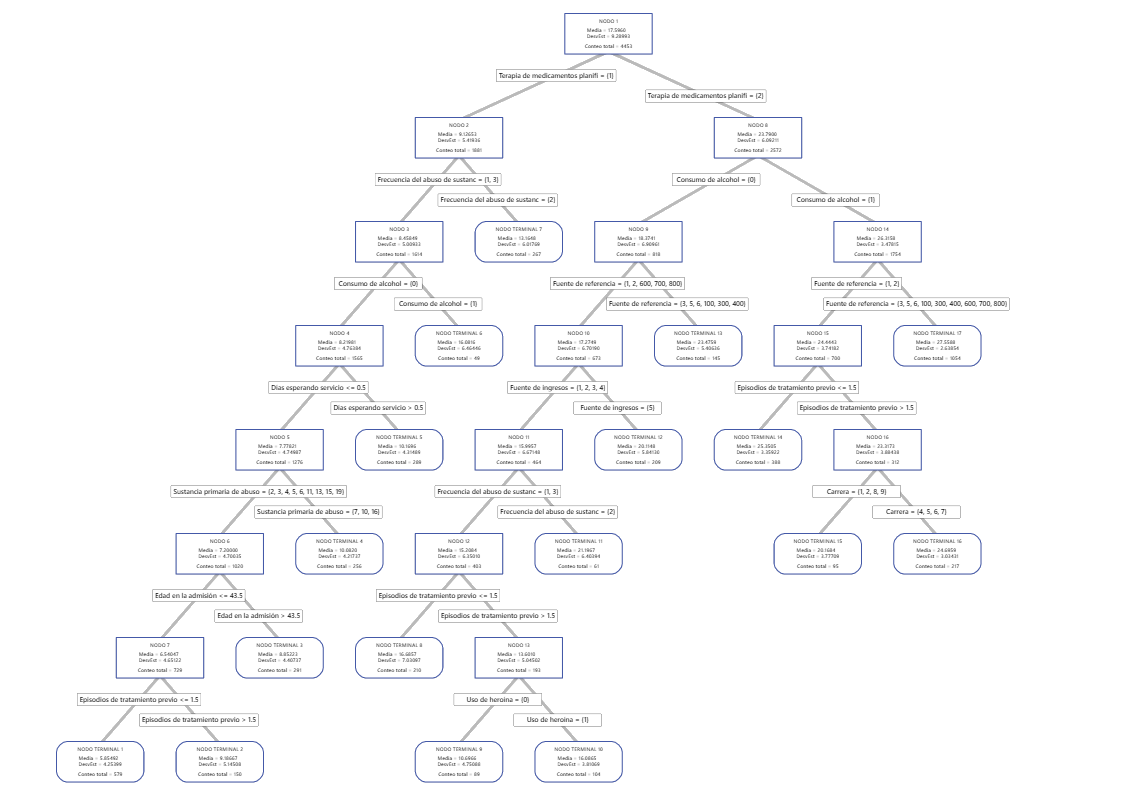
Para un análisis con validación cruzada de k pliegues, el diagrama de árbol muestra los 4453 casos del conjunto de datos completo. Puede alternar las vistas del árbol entre la vista dividida detallada y la vista de dividida de nodos. La tabla de ajustes y estadísticas de errores y los criterios para clasificar los sujetos proporcionan información adicional sobre los nodos terminales.
- Nodo 2 incluye los casos donde 'Terapia de medicamentos planificada' = 1. Este nodo tiene 1881 casos. La media del nodo es menor que la media general. La desviación estándar para Nodo 2 es aproximadamente 5.4, que es menor que la desviación estándar general porque una división produce nodos más puros.
- Nodo 8 incluye los casos donde 'Terapia de medicamentos planificada' = 2. Este nodo tiene 2572 casos. La media para el nodo es mayor que la media general. La desviación estándar para Nodo 8 es aproximadamente 6.1, que también es menor que la desviación estándar general.
A continuación, el nodo 2 se divide por 'Frecuencia del abuso de sustancias' y el nodo 8 se divide por el 'Consumo de alcohol'. El nodo terminal 17 tiene los casos para 'Terapia de medicamentos planificada' = 2, 'Consumo de alcohol' = 1 y 'Fuente de referencia' = 3, 5, 6, 100, 300, 400, 600, 700 u 800. Los investigadores señalan que Nodo terminal 17 tiene la media más alta, la desviación estándar más pequeña y la mayoría de los casos.
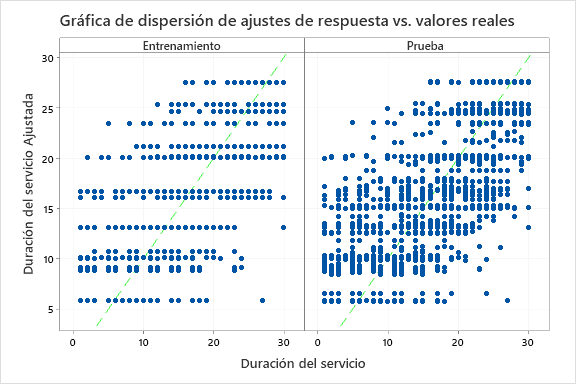
Los resultados incluyen una gráfica de dispersión de los valores de respuesta ajustados y los valores de respuesta reales. Los puntos del conjunto de datos de entrenamiento y del conjunto de datos de prueba muestran patrones similares. Esta similitud sugiere que el rendimiento del árbol en nuevos datos está cerca del rendimiento del árbol en los datos de entrenamiento.
- 'Terapia de medicamentos planificada' = {2}
- 'Consumo de alcohol' = {0}
- 'Fuente de referencia' = {1, 2, 600, 700, 800}
- 'Fuente de ingresos' = {1, 2, 3, 4}
- 'Frecuencia del abuso de sustancias' = {1, 3}
- 'Episodios de tratamiento previos' <= 1.5
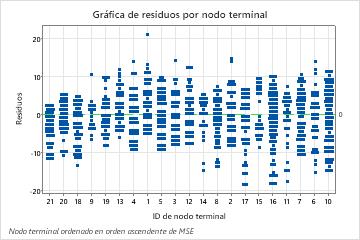
La gráfica de los residuos por nodo terminal muestra que el ajuste es demasiado grande para un pequeño grupo de pacientes en Nodo terminal 8. Los analistas consideran una investigación sobre por qué algunos de estos pacientes utilizan los servicios durante menos tiempo que un paciente típico en su grupo. Por ejemplo, si estos pacientes se encuentran en una ubicación geográfica diferente de los otros pacientes en el nodo terminal, entonces diferentes regulaciones gubernamentales y de seguros podrían afectar cuánto tiempo utilizan los servicios.
La gráfica de los residuos por nodo terminal muestra otros casos en los que los analistas pueden elegir investigar conglomerados o valores atípicos. Por ejemplo, en estos datos, hay un residuo que aparece mucho más grande que los demás en Nodo de terminal 1 y en Nodo de terminal 7. Los analistas deciden investigar la razón por la que estos pacientes utilizaron servicios durante más tiempo que otros pacientes en su nodo terminal.
Debido a que el valor de prueba R2 deja margen de mejora y las parcelas residuales muestran casos en los que el árbol no encaja bien, los investigadores consideran si usar a Regresión TreeNet® o a Regresión Random Forests® para tratar de mejorar el ajuste.