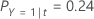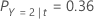Un árbol de clasificación resulta de una partición recursiva binaria del conjunto de datos de entrenamiento original. Cualquier nodo primario (un subconjunto de datos de entrenamiento) de un árbol se puede dividir en dos nodos secundarios mutuamente excluyentes de un número finito de formas, que depende de los valores de datos reales recopilados en el nodo.
El procedimiento de división trata las variables predictoras como continuas o categóricas. Para una variable continua X y un valor c, se define una división enviando todos los registros con los valores de X menores o iguales que c al nodo izquierdo y todos los registros restantes al nodo derecho. CART siempre utiliza el promedio de dos valores adyacentes para calcular c. Una variable continua con N valores distintos genera hasta N–1 divisiones potenciales del nodo primario (el número real será menor cuando se impongan límites en el tamaño mínimo permitido del nodo).
Por ejemplo, un predictor continuo tiene los valores 55, 66 y 75 en los datos. Una división posible para esta variable es enviar todos los valores menores o iguales que (55+66)/2 a 60,5 a un nodo secundario y todos los valores mayores que 60,5 al otro nodo secundario. Los casos con el valor predictor de 55 van a un nodo y los casos con los valores 66 y 75 van al otro nodo. La otra división posible para este predictor es enviar todos los valores menores o iguales a 70,5 a un nodo secundario y valores superiores a 70,5 al otro nodo. Los casos con los valores 55 y 66 van a un nodo, y los casos con el valor 75 van al otro nodo.
Para una variable categórica X con valores distintos .1c2, …, ckUna división se define como un subconjunto de niveles que se envían al nodo secundario izquierdo. Una variable categórica con niveles K genera hasta 2K-1–1 divisiones.
| Nodo infantil izquierdo | Nodo de niño correcto |
|---|---|
| Rojo, Azul | Amarillo |
| Rojo, Amarillo | Azul |
| Azul, Amarillo | Rojo |
En los árboles de clasificación, el destino es multinomio con clases distintas K. El objetivo principal del árbol es encontrar una manera de separar diferentes clases de destino en nodos individuales de la manera más pura posible. El número resultante de nodos terminales no necesita ser K; se pueden utilizar varios nodos de terminal para representar una clase de destino específica. Un usuario puede especificar probabilidades previas para las clases de destino; estos serán contabilizados por CART durante el proceso de cultivo de árboles.
En las siguientes secciones, Minitab utiliza las siguientes definiciones para una variable de respuesta binaria:
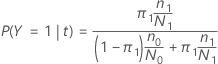
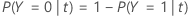
En las siguientes secciones, Minitab utiliza las siguientes definiciones para una variable de respuesta multinomial:
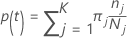
Probabilidad de la clase = %1 j nodo dado t:
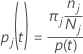
Estas definiciones proporcionan las probabilidades dentro del nodo. Minitab calcula estas probabilidades para cualquier nodo y cualquier división potencial. Minitab calcula la mejora general de una posible división de estas probabilidades con uno de los siguientes criterios.
Notación
| Término | Description |
|---|---|
| K | número de clases en la variable de respuesta |
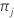 | probabilidad previa para la clase j |
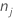 | número de observaciones para la clase j en un nodo |
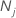 | número de observaciones para la clase j en los datos |
Criterio Gini
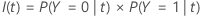
La siguiente fórmula más general se aplica a una variable de respuesta multinomial:
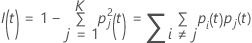
Tenga en cuenta que si todas las observaciones de un nodo están en una
clase,  .
.
Criterio de entropía
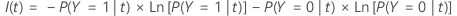
La siguiente fórmula más general se aplica a una variable de respuesta multinomial:

Tenga en cuenta que si todas las observaciones de un nodo están en una
clase,  .
.
Criterio de dosis
| Super Clase 1 | Super Clase 2 |
|---|---|
| %1, 2, 3 %2 %3, %4 %5 | 4 |
| %1, 2, 3 %2 %3, %4 %5 | 3 |
| %1, 3, 4 %2 = %3@, %4 = %5 | 2 |
| %2, 3, 4 %2 = %3@, %4 = %5 | 1 |
| %1, 2 %2 = %3@, %4 = %5 | 3, 4 |
| %1, 3 %2 = %3@, %4 = %5 | %2, 4 %2 = %3@, %4 = %5 |
| %1, 4 %2 = %3@, %4 = %5 | %2, 3 %2 = %3@, %4 = %5 |


La superclase izquierda tiene todas las clases de destino que tienden a ir a la izquierda. La superclase correcta tiene todas las clases objetivo que tienden a ir a la derecha.
| Clase | Probabilidad de nodo infantil izquierdo | Probabilidad de nodo infantil correcto |
|---|---|---|
| 1 | 0.67 | 0.33 |
| 2 | 0.82 | 0.18 |
| 3 | 0.23 | 120.77 |
| 4 | 0.89 | 0.11 |
A continuación, la mejor manera de hacer las superclases para la división candidata es asignar el número 1, 2, 4 o como una superclase y el 3 o como la otra superclase.
El resto del cálculo es el mismo que el criterio for the Gini con las superclases como destino binario.
Cálculo de mejora de los criterios
Después de que Minitab calcule la impureza del nodo, Minitab calcula las probabilidades condicionales para dividir el nodo con un predictor:
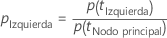
y

A continuación, la mejora de una división es de la siguiente fórmula:
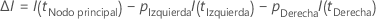
La división con el valor de mejora más alto se convierte en parte del árbol. Si la mejora para dos predictores es la misma, el algoritmo requiere una selección para continuar. La selección utiliza un esquema de desempate determinista que implica la posición de los predictores en la hoja de trabajo, el tipo de predictor y el número de clases en un predictor categórico.
Probabilidad de clase
Las divisiones de nodo maximizan la probabilidad de una clase dentro de un nodo determinado.
Nodos terminales
- El número de casos en el nodo alcanza el tamaño mínimo para el análisis. El mínimo predeterminado en Minitab Statistical Software es 3.
- Todos los casos de un nodo tienen la misma clase de respuesta.
- Todos los casos de un nodo tienen los mismos valores predictores.
Clase prevista para un nodo terminal
La clase pronosticada para un nodo de terminal es la clase que minimiza el costo de clasificación incorrecta para el nodo. Las representaciones del coste de clasificación incorrecta dependen del número de clases de la variable de respuesta. Dado que la clase predicha para un nodo de terminal procede de los datos de entrenamiento cuando se utiliza un método de validación, todas las fórmulas siguientes usan probabilidades del conjunto de datos de entrenamiento.
Variable de respuesta: %1
La siguiente ecuación proporciona el costo de clasificación errónea para la predicción de que los casos en el nodo son la clase de evento:

La siguiente ecuación proporciona el costo de clasificación errónea para la predicción de que el caso en el nodo es la clase que no es de evento:

| Término | Description |
|---|---|
| PY=0|t | probabilidad condicional de que un caso en el nodo t pertenece a la clase que no es de evento |
| C1|0 | costo de clasificación errónea que un caso de clase sin evento se predice como un caso de clase de evento |
| PY=1|t | probabilidad condicional de que un caso en el nodo t pertenece a la clase de evento |
| C0|1 | costo de clasificación errónea que un caso de clase de evento se predice como un caso de clase sin evento |
La clase pronosticada para un nodo terminal es la clase con el coste mínimo de clasificación incorrecta.
Variable de respuesta multinomial

Por ejemplo, considere una variable de respuesta con tres clases y los siguientes costos de clasificación errónea:
| Clase de predicción | |||
| Clase real | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
A continuación, considere que las clases de la variable de respuesta tienen las siguientes probabilidades para el nodo t:
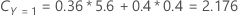

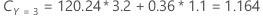
El menor costo de clasificación errónea es para la predicción de que Y = 3, 1.164. Esta clase es la clase predicha para el nodo terminal.