Predictores importantes
Cualquier árbol de clasificación es una colección de divisiones. Cada división proporciona una mejora al árbol. Cada división también incluye divisiones sustitutas que también proporcionan mejoras al árbol. La importancia de una variable viene dada por todas sus mejoras cuando el árbol utiliza la variable para dividir un nodo o como sustituta para dividir un nodo cuando otra variable tiene un valor faltante.
La siguiente fórmula proporciona la mejora en un solo nodo:
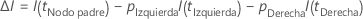
Los valores de I(t), pIzquierda y pDerecha dependen del criterio empleado para dividir los nodos. Para obtener más información, vaya a Método de división de nodos: Clasificación CART®.
Log-verosimilitud promedio
Datos de entrenamiento o sin validación
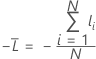
donde
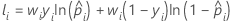
Notación para datos de entrenamiento o sin validación
| Término | Description |
|---|---|
| N | tamaño de muestra de los datos completos o los datos de entrenamiento |
| wi | ponderación para la iésima observación en el conjunto de datos completo o de entrenamiento |
| yi | variable indicadora que es 1 para el evento y 0 de lo contrario para el conjunto de datos completo o de entrenamiento |
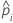 | probabilidad pronosticada del evento para la iésima fila en el conjunto de datos completo o de entrenamiento |
Validación cruzada con k-fold
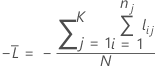
donde
Notación para la validación cruzada con k-fold
| Término | Description |
|---|---|
| N | tamaño de la muestra de los datos completos o de entrenamiento |
| nj | tamaño de muestra del pliegue j |
| wij | ponderación para la iésima observación en el grupo j |
| yij | variable indicadora que es 1 para el evento y 0 en caso contrario para los datos en el pliegue j |
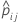 | probabilidad pronosticada del evento a partir de la estimación del modelo que no incluye las observaciones para la iésima observación en el grupo j |
Conjunto de datos de prueba
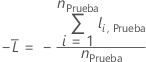
donde
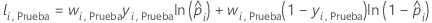
Notación para el conjunto de datos de prueba
| Término | Description |
|---|---|
| nPrueba | tamaño de la muestra del conjunto de prueba |
| wi, Prueba | ponderación para la iésima observación en el conjunto de datos de prueba |
| yi, Prueba | variable que indica 1 para el evento y 0 para los datos del conjunto de prueba |
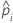 | probabilidad pronosticada del evento para la iésima fila en el conjunto de prueba |
Área bajo la curva ROC
Fórmula
Para el área debajo de la curva, Minitab utiliza una integración.
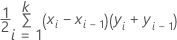
donde k es el número de nodos terminales y (x0, y0) es el punto (0, 0).
| x (tasa de falsos positivos) | y (tasa de verdaderos positivos) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
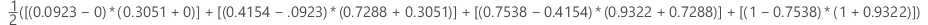
Notación
| Término | Description |
|---|---|
| TRP | tasa de verdaderos positivos |
| FPR | tasa de falsos positivos |
| TP | verdadero positivo, eventos que fueron evaluados correctamente |
| P | número de eventos positivos reales |
| FP | negativos verdaderos, no eventos que fueron evaluados correctamente |
| N | número de eventos negativos reales |
| FNR | tasa de falsos negativos |
| TNR | tasa de verdaderos negativos |
IC del 95% para el área bajo la curva ROC
El siguiente intervalo proporciona los límites superior e inferior para el intervalo de confianza:
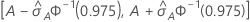
El cálculo del error estándar del área bajo la curva ROC (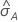
) proviene de Salford Predictive Modeler®. Para obtener información general sobre la estimación de la varianza del área bajo la curva ROC, véase las siguientes referencias:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. y Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G. y Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
Notación
| Término | Description |
|---|---|
| A | área bajo la curva ROC |
 | 0.975 percentil de la distribución normal estándar |
Elevación
Fórmula
Para el 10% de las observaciones en los datos con las mayores probabilidades de ser asignados a la clase de evento, utilice la siguiente fórmula.
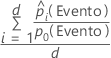
Para la elevación de pruebas con un conjunto de datos de prueba, utilice observaciones del conjunto de datos de prueba. Para la elevación de prueba con validación cruzada de k-fold, seleccione los datos que desea utilizar y calcule la elevación a partir de las probabilidades pronosticadas para los datos que no están en la estimación del modelo.
Notación
| Término | Description |
|---|---|
| d | número de casos en el 10% de los datos |
 | probabilidad pronosticada del evento |
 | probabilidad del evento en los datos de entrenamiento o, si el análisis no utiliza ninguna validación, en el conjunto de datos completo |
Costo de clasificación errónea
El costo de clasificación errónea en la tabla de resumen del modelo es el costo de clasificación errónea relativo para el modelo en relación con un clasificador trivial que clasifica todas las observaciones en la clase más frecuente.
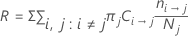
El costo de clasificación errónea relativo tiene la siguiente forma:
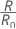
Donde R0 es el costo del clasificador trivial.
La fórmula de R simplifica cuando las probabilidades a priori son iguales o provienen de los datos.
Probabilidades a priori iguales
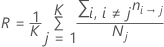
Probabilidades a priori de los datos
Con esta definición, R tiene la siguiente forma:
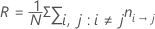
Notación
| Término | Description |
|---|---|
| πj | probabilidad a priori de lajésima clase de la variable de respuesta |
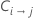 | costo de clasificar erróneamente la clase i como clase j |
 | número de registros de clase i clasificados erróneamente como clase j |
| Nj | número de casos en la clase jésima de la variable de respuesta |
| K | número de clases en la variable de respuesta |
| N | número de casos en los datos |
