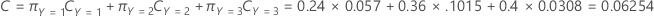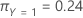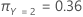Métodos y fórmulas para la clasificación errónea en Clasificación CART^®

Seleccione el método o la fórmula de su elección.

En este tema

Conteo
Conteo ponderado
% Error
Costo

La tabla de clasificación errónea no está presente cuando el método de división es la probabilidad de clase.

Conteo

Cuando no hay ponderaciones, los conteos y los tamaños de muestra son iguales.

Conteo ponderado

En el caso ponderado, el conteo ponderado es la suma de las ponderaciones de una categoría. Conteo ponderado redondeado al número entero más cercano. Utilice las ponderaciones sin redondeo para calcular los porcentajes y las tasas. Considere el siguiente ejemplo simple:

Nivel de respuesta	Nivel pronosticado	Ponderación
Sí	Sí	0.1
Sí	Sí	0.2
Sí	No	0.3
Sí	No	0.4
No	No	0.5
No	No	0.6
No	Sí	0.7
No	Sí	0.8

Esta tabla proporciona las siguientes estadísticas:

Clase real	Conteo ponderado	Clasificación errónea	Clase pronosticada = No	Porcentaje correcto
Sí	0.1 + 0.2 + 0.3 + 0.4 = 1	0.1 + 0.2 = 0.3 ≈ 0	0.3 + 0.4 = 0.7 ≈ 1	(0.3 / 1.0) ×100 = 30%
No	0.5 + 0.6 + 0.7 + 0.8 = 2.6 ≈ 3	0.7 + 0.8 = 1.5 ≈ 2	0.5 + 0.6 = 1.1 ≈ 1	1.1 / 2.6) × 100 = 42.31%
Todos	1 + 2.6 = 3.6 ≈ 4	0.3 + 1.5 = 1.8 ≈ 2	0.7 + 1.1 = 1.8 ≈ 2	(0.3 + 1.1) / 3.6 × 100 = 38.89%

% Error

En el caso ponderado, utilice conteos ponderados en lugar de conteos.

Costo

El cálculo del costo depende de si la variable de respuesta es binaria o multinomial.

Costo (% Error ? Costo de clasificación errónea de entrada para la clase) / 100

Variable de respuesta binaria

La ecuación siguiente proporciona el costo de la clase de evento:

La ecuación siguiente proporciona el costo para la clase de no evento:

La siguiente ecuación proporciona el costo total para todas las clases:

Variable de respuesta multinomial

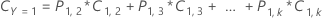
Para el caso multinomial, la ecuación extiende la fórmula de la variable de respuesta binaria para tener en cuenta todos los tipos posibles de clasificaciones erróneas. Por ejemplo, para una respuesta multinómica con clases k, el costo de clasificación errónea para Y = 1 utiliza la siguiente ecuación:

La siguiente ecuación proporciona el costo total para el caso multinomial:

Por ejemplo, considere una variable de respuesta con 3 clases y los siguientes costos de clasificación errónea:

	Clase de predicción
Clase real	1	2	3
1	0.0	4.1	3.2
2	5.6	0.0	1.1
3	0.4	0.9	0.0

A continuación, tenga en cuenta que la tabla siguiente proporciona los porcentajes de error:

	Clase de predicción
Clase real	1	2	3
1	N/A	1%	0.5%
2	1.4%	N/A	2.1%
3	5%	1.2%	N/A

Por último, tenga en cuenta que las clases de la variable de respuesta tienen las siguientes probabilidades a priori:

Las siguientes ecuaciones proporcionan los costos asociados con la clasificación errónea para cada clase en la variable de respuesta:

La siguiente ecuación proporciona el costo total:

Nivel de respuesta	Nivel pronosticado	Ponderación
Sí	Sí	0.1
Sí	Sí	0.2
Sí	No	0.3
Sí	No	0.4
No	No	0.5
No	No	0.6
No	Sí	0.7
No	Sí	0.8

Nivel de respuesta	Nivel pronosticado	Ponderación
Sí	Sí	0.1
Sí	Sí	0.2
Sí	No	0.3
Sí	No	0.4
No	No	0.5
No	No	0.6
No	Sí	0.7
No	Sí	0.8

Métodos y fórmulas para la clasificación errónea en Clasificación CART®