En este tema
Paso 1: Investigar árboles alternativos
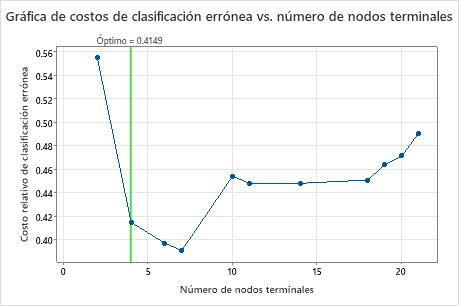
La gráfica Costo de clasificación errónea vs. Número de nodos terminales muestra el costo de clasificación errónea para cada árbol de la secuencia que produce el árbol óptimo. Por opción predeterminada, el árbol óptimo inicial es el árbol más pequeño con un costo de clasificación errónea dentro de un error estándar del árbol que minimiza el costo de clasificación errónea. Cuando el análisis utiliza la validación cruzada o un conjunto de datos de prueba, el costo de clasificación errónea procede del ejemplo de validación. Los costos de clasificación errónea para la muestra de validación normalmente se nivelan y, finalmente, aumentan a medida que el árbol crece.
- El árbol óptimo forma parte de un patrón cuando los costos de clasificación errónea disminuyen. Uno o más árboles que tienen algunos nodos más forman parte del mismo patrón. Normalmente, desea realizar predicciones desde un árbol con la mayor exactitud de predicción posible. Si el árbol es lo suficientemente simple, también puede usarlo para comprender cómo afecta cada variable predictora a los valores de respuesta.
- El árbol óptimo forma parte de un patrón cuando los costos de clasificación errónea son relativamente planos. Uno o más árboles con estadísticas de resumen del modelo similares tienen muchos menos nodos que el árbol óptimo. Normalmente, un árbol con menos nodos terminales proporciona una imagen más clara de cómo cada variable predictora afecta a los valores de respuesta. Un árbol más pequeño también facilita la identificación de algunos grupos objetivo para estudios posteriores. Si la diferencia en la exactitud de predicción para un árbol más pequeño es insignificante, también puede utilizar el árbol más pequeño para evaluar las relaciones entre la respuesta y las variables predictoras.
Resumen del modelo
| Total de predictores | 13 |
|---|---|
| Predictores importantes | 13 |
| Número de nodos terminales | 4 |
| Tamaño mínimo del nodo terminal | 27 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| Logverosimilitud promedio | 0.4772 | 0.5164 |
| Área bajo la curva ROC | 0.8192 | 0.8001 |
| IC de 95% | (0.3438, 1) | (0.7482, 0.8520) |
| Elevación | 1.6189 | 1.8849 |
| Costo de clasificación errónea | 0.3856 | 0.4149 |
Resultados clave: Gráfica y resumen del modelo para árbol con 4 nodos
El árbol de la secuencia con 4 nodos tiene un costo de clasificación errónea cercano a 0.41. El patrón cuando el costo de clasificación errónea disminuye continúa después del árbol de 4 nodos. En un caso como este, los analistas eligen explorar algunos de los otros árboles simples que tienen menores costos de clasificación errónea.
Resumen del modelo
| Total de predictores | 13 |
|---|---|
| Predictores importantes | 13 |
| Número de nodos terminales | 7 |
| Tamaño mínimo del nodo terminal | 5 |
| Estadísticas | Entrenamiento | Prueba |
|---|---|---|
| Logverosimilitud promedio | 0.3971 | 0.5094 |
| Área bajo la curva ROC | 0.8861 | 0.8200 |
| IC de 95% | (0.5590, 1) | (0.7702, 0.8697) |
| Elevación | 1.9376 | 1.8165 |
| Costo de clasificación errónea | 0.2924 | 0.3909 |
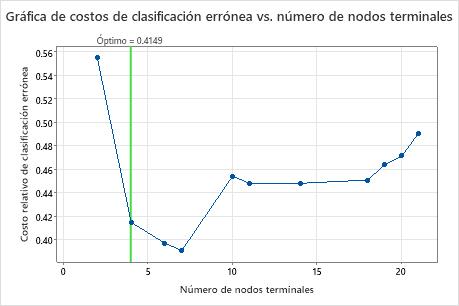
Resultados clave: Gráfica y resumen del modelo para árbol con 7 nodos
El árbol de clasificación que minimiza el costo de clasificación errónea con validación cruzada relativo tiene 7 nodos terminales y un costo de clasificación errónea relativo de aproximadamente 0.39. Otros estadísticos, como el área bajo la curva ROC, también confirman que el árbol de 7 nodos funciona mejor que el árbol de 4 nodos. Dado que el árbol de 7 nodos tiene pocos nodos que también es fácil de interpretar, los analistas deciden utilizar el árbol de 7 nodos para estudiar las variables importantes y realizar predicciones.
Paso 2: Investigue los nodos terminales más puros en el diagrama de árbol
Después de seleccionar un árbol, investigue los nodos terminales más puros del diagrama. Azul representa el nivel de evento y Rojo representa el nivel de no evento.
Nota
Puede hacer clic con el botón derecho en el diagrama de árbol para mostrar la vista de división de nodo del árbol. Esta vista es útil cuando tiene un árbol grande y desea ver solo las variables que dividen los nodos.
Los nodos continúan dividiéndose hasta que los nodos terminales no se pueden dividir en agrupaciones adicionales. Los nodos que son en su mayoría azules indican una proporción fuerte del nivel de evento. Los nodos que son en su mayoría rojos indican una proporción fuerte del nivel de no evento.
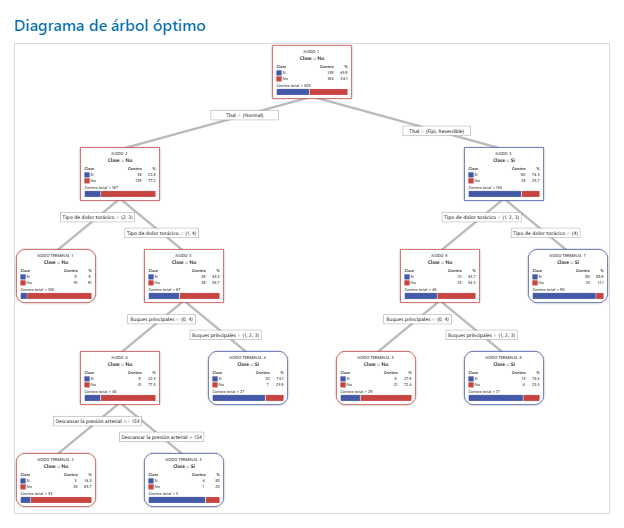
Resultado clave: Diagrama de árbol
Este árbol de clasificación tiene 7 nodos terminales. Azul es para el nivel de evento (Sí) y Rojo es para el nivel de no evento (No). El diagrama de árbol utiliza el conjunto de datos de entrenamiento. Puede alternar las vistas del árbol entre la vista dividida detallada y la vista de dividida de nodos.
- Nodo 2: THAL fue Normal para 167 casos. De los 167 casos, 38 o 22.8% son Sí, y 129 o 77.2% son No.
- Nodo 5: THAL fue Fijo o Reversible para 136 casos. De los 136 casos, 101 o 74.3% son Sí, y 35 o 25.7% son No.
El siguiente divisor para el nodo hijo izquierdo y el nodo hijo derecho es Tipo de dolor de pecho, donde el dolor se clasifica como 1, 2, 3 o 4. Nodo 2 es el padre de Nodo de terminal 1, y Nodo 5 es el padre de Nodo de terminal 7.
- Nodo terminal 1: Para 100 casos, THAL fue Normal, y Dolor en el pecho fue de 2 o 3. De los 100 casos, 9 o 9% son Sí, y 91 o 91% son No.
- Nodo terminal 7: Para 90 casos, THAL fue Fijo o Reversible, y Dolor en el pecho fue de 4. De los 90 casos, 80 u 88.9% son Sí, y 10 o 11.1% son No.
Paso 3: Determinar las variables importantes
Utilice el gráfico de importancia de variable relativa para determinar qué predictores son las variables más importantes para el árbol.
Las variables importantes son divisores primarios o sustitutos en el árbol. La variable con la puntuación de mejora más alta se establece como la variable más importante, y las otras variables se clasifican en consecuencia. La Importancia relativa de las variables estandariza los valores de importancia para facilitar la interpretación. La importancia relativa se define como la mejora porcentual con respecto al predictor más importante.
Los valores de importancia relativa de la variable oscilan entre 0% y 100%. La variable más importante siempre tiene una importancia relativa de 100%. Si una variable no está en el árbol, esa variable no es importante.
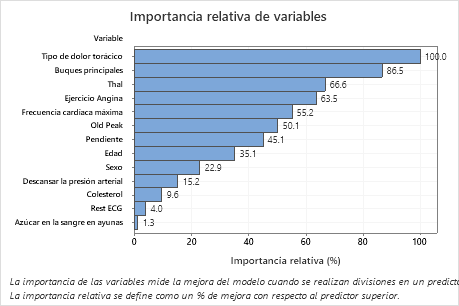
Resultado clave: Importancia relativa de variables
- Buques principales es aproximadamente 87% tan importante como Tipo de dolor torácico.
- Thal y Ejercicio Angina ambos son aproximadamente un 65% tan importantes como Tipo de dolor torácico.
- Frecuencia cardíaca máxima es aproximadamente 55% tan importante como Tipo de dolor torácico.
- Old Peak es aproximadamente 50% tan importante como Tipo de dolor torácico.
- Pendiente, , Edad Sexo, y Descansar la presión arterial son mucho menos importantes que Tipo de dolor torácico.
Aunque tienen una importancia positiva, los analistas podrían decidir que Colesterol, Rest ECG, y Azúcar en la sangre en ayunas no son contribuyentes importantes al árbol.
Paso 4: Evalúe el poder predictivo de su árbol
El árbol más preciso es el que tiene el menor costo de clasificación errónea. A veces, los árboles más simples con costos de clasificación errónea ligeramente más altos funcionan igual de bien. Puede utilizar la gráfica Costo de clasificación errónea frente a nodos terminales para identificar árboles alternativos.
La curva de rendimiento de diagnóstico (ROC) muestra qué tan bien clasifica los datos un árbol. La curva ROC grafica la tasa de verdaderos positivos en el eje Y y la tasa de falsos positivos en el eje X. La tasa de verdaderos positivos también se conoce como potencia. La tasa de falsos positivos también se conoce como error tipo I.
Cuando un árbol de clasificación puede separar perfectamente las categorías en la variable de respuesta, el área bajo la curva ROC es 1, que es el mejor modelo de clasificación posible. Alternativamente, si un árbol de clasificación no puede distinguir categorías y realiza asignaciones de forma totalmente aleatoria, el área bajo la curva ROC es 0.5.
Cuando utiliza una técnica de validación para construir el árbol, Minitab proporciona información sobre el rendimiento del árbol en los datos de entrenamiento y validación (prueba). Cuando las curvas están juntas, puede estar más seguro de que el árbol no está sobreajustado. El rendimiento del árbol con los datos de prueba indica qué tan bien el árbol puede predecir nuevos datos.
- Tasa de verdaderos positivos (TPR): la probabilidad de que un caso de evento se pronostique correctamente
- Tasa de falsos positivos (FPR) — la probabilidad de que un caso de no evento se pronostique erróneamente
- Tasa de falsos negativos (FNR) — la probabilidad de que un caso de evento se pronostique erróneamente
- Tasa de verdaderos negativos (TNR): la probabilidad de que un caso de no evento se pronostique correctamente
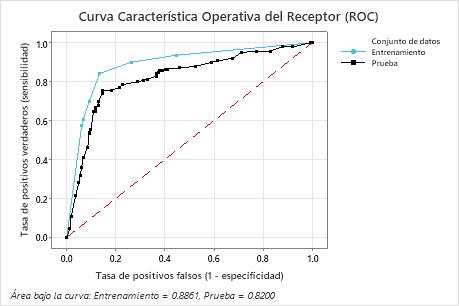
Resultado clave: Curva de rendimiento diagnóstico (ROC)
Para este ejemplo, el área bajo la curva ROC es 0.886 para Entrenamiento y 0.82 para Prueba. Estos valores indican que el árbol de clasificación es un clasificador razonable, en la mayoría de las aplicaciones.
Matriz de confusión
| Clase de predicción (entrenamiento) | Clase de predicción (prueba) | ||||||
|---|---|---|---|---|---|---|---|
| Clase real | Conteo | Sí | No | % Correcto | Sí | No | % Correcto |
| Sí (Evento) | 139 | 117 | 22 | 84.2 | 105 | 34 | 75.5 |
| No | 164 | 22 | 142 | 86.6 | 24 | 140 | 85.4 |
| Todo | 303 | 139 | 164 | 85.5 | 129 | 174 | 80.9 |
| Estadísticas | Entrenamiento (%) | Prueba (%) |
|---|---|---|
| Tasa de positivos verdaderos (sensibilidad o potencia) | 84.2 | 75.5 |
| Tasa de positivos falsos (error tipo I) | 13.4 | 14.6 |
| Tasa de negativos falsos (error tipo II) | 15.8 | 24.5 |
| Tasa de negativos verdaderos (especificidad) | 86.6 | 85.4 |
Resultado clave: Matriz de confusión
- Tasa de verdaderos positivos (TPR): 84,2% para los datos de Entrenamiento y 75,5% para los datos de Prueba
- Tasa de falsos positivos (FPR) — 13,4% para los datos de Entrenamiento y 14,6% para los datos de Prueba
- Tasa de falsos negativos (FNR) — 15,8% para los datos de Entrenamiento y 24,5% para los datos de Prueba
- Tasa de verdaderos negativos (TNR) — 86,6% para los datos de Entrenamiento y 85,4% para los datos de Prueba
En general, el %Correcto para los datos de entrenamiento es 85.5%, y 80.9% para los datos de prueba.
