Una probabilidad posterior es la probabilidad de asignar observaciones a grupos dados los datos. Una probabilidad previa es la probabilidad de que una observación pertenezca a un grupo antes de recoger los datos. Por ejemplo, si clasifica a los compradores de un vehículo en particular, usted ya podría saber que el 60% de los compradores son hombres y el 40% son mujeres. Si usted conoce o puede estimar estas probabilidades, un análisis discriminante puede utilizar estas probabilidades previas en el cálculo de las probabilidades posteriores. Cuando usted no especifica las probabilidades previas, Minitab presupone que los grupos son igualmente probables.
Con el supuesto de que los datos tienen una distribución normal, la función discriminante lineal aumenta en ln(pi), donde pi es la probabilidad previa del grupo i. Puesto que las observaciones son asignadas a los grupos según la distancia generalizada más pequeña o, equivalentemente, según la función discriminante lineal más grande, el efecto es aumentar las probabilidades posteriores para un grupo con una alta probabilidad previa.
Nota
Especificar las probabilidades previas puede incidir enormemente en la exactitud de los resultados. Investigue si la desigualdad en las proporciones de los grupos refleja una diferencia real en la población real o si la diferencia se debe a un error de muestreo.
Ahora, supongamos que tenemos probabilidades previas y supongamos que fi(x) es la densidad conjunta para los datos del grupo i (con los parámetros de población reemplazados por las estimaciones de la muestra).
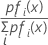
La probabilidad posterior más grande es equivalente al valor más grande de ln [pifi(x)]
Si fi(x) es la distribución normal, entonces:
ln [pifi(x)] = -0.5 [di2(x) – 2 ln pi] – (una constante)
El término entre corchetes se denomina distancia al cuadrado generalizada de x al grupo i y se denota mediante di2(x). Observe,
di2(x) = -2[mi' Sp-1 x - 0.5 mi' Sp-1mi + ln pi] + x' Sp-1x
El término entre corchetes es la función discriminante lineal. La única diferencia con respecto al caso en el que no hay probabilidades previas es un cambio en el término constante. Observe que la probabilidad posterior más grande es equivalente a la distancia generalizada más pequeña, la cual es equivalente a la función discriminante lineal más grande.
