En este tema
Método de componentes principales
En el análisis de componentes principales, Minitab primero halla el conjunto de vectores propios ortogonales de la matriz de correlación o de covarianzas de las variables. La matriz de componentes principales es el producto de la matriz de vectores propios por la matriz de variables independientes. El primer componente principal representa el mayor porcentaje de la variación total de los datos. El segundo componente principal representa el segundo mayor porcentaje de la variación total de los datos, y así sucesivamente. La meta de los componentes principales consiste en explicar la máxima cantidad de varianza con el menor número de componentes.
No unicidad de los coeficientes
Los coeficientes para los componentes principales son únicos (excepto por un cambio en el signo) si los valores propios son distintos y no son cero. Si un valor propio se repite, el "espacio abarcado" por todos los vectores de los componentes principales correspondientes al mismo valor propio es único, pero los vectores individuales no lo son. Por lo tanto, los coeficientes que Minitab muestra en la salida y los que aparecen en libros o en otro programa pudieran no coincidir, aunque los valores propios (varianzas de los componentes) siempre serán los mismos.
Si la matriz de covarianzas tiene rango r < p, donde p es el número de variables, entonces habrá valores propios p – r iguales a cero. Los vectores propios que corresponden a estos valores propios pudieran no ser únicos. Esto puede suceder si el número de observaciones es menor que p o si hay multicolinealidad.
Vectores propios
Los vectores propios, compuestos por los coeficientes que corresponden a cada variable, son las ponderaciones para cada variable utilizadas para calcular las puntuaciones de los componentes principales. Los vectores propios se obtienen como las columnas de la matriz ortogonal en la descomposición espectral de la matriz de covarianzas o de correlación, S o R. Más específicamente, debido a que R es simétrica, existe una matriz ortogonal V tal que V'RV = D o, de forma equivalente, R = VDV', donde D es una matriz diagonal cuyos elementos diagonales son los valores propios. Los vectores propios son las columnas de V. Los vectores propios se originan de R = VDV'.
Notación
| Término | Description |
|---|---|
| R | matriz de correlación |
| V | matriz de vectores propios |
| D | matriz diagonal de valores propios |
Puntuaciones
Fórmula
Las puntuaciones son las combinaciones lineales de las variables originales que explican la varianza en los datos.
Las puntuaciones se calculan de la siguiente manera: Z = YV
Notación
| Término | Description |
|---|---|
| Z | matriz de las puntuaciones de los componentes principales (n × m) |
| Y | matriz de datos estandarizados (n × p) utilizada con el método de matriz de correlación |
| V | matriz de vectores propios (p × m) |
Nota
Si usted utiliza el método de matriz de covarianzas en lugar del método de matriz de correlación (el predeterminado), entonces Minitab usa la matriz de datos sin procesar para Y en lugar de la matriz de datos estandarizados.
Valor propio
Fórmula
Los valores propios son los elementos diagonales de la matriz diagonal en la descomposición espectral de la matriz de covarianzas o de correlación (vea el tema "Vectores propios"). Los valores propios también representan las varianzas de las muestras de los componentes principales Z = V Y.
Notación
| Término | Description |
|---|---|
| Z | matriz de las puntuaciones de los componentes principales (n × m) |
| Y | matriz de datos estandarizados (n × p) utilizada con el método de matriz de correlación |
| V | matriz de vectores propios (p × m) |
Nota
Si usted utiliza el método de matriz de covarianzas en lugar del método de matriz de correlación (el predeterminado), entonces Minitab usa la matriz de datos sin procesar para Y en lugar de la matriz de datos estandarizados.
Proporción
Fórmula
La proporción de varianza de la muestra explicada por el késimo componente principal se calcula de la siguiente manera:
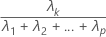
Notación
| Término | Description |
|---|---|
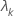 | el késimo valor propio |
| p | el número de variables |
Proporción acumulada
Fórmula
La proporción acumulada de la varianza de la muestra explicada por los primeros k componentes principales se calcula de la siguiente manera: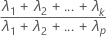
Notación
| Término | Description |
|---|---|
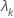 | el késimo valor propio |
| p | el número de variables |
Distancia de Mahalanobis
Fórmula


Cuando n – p – 1 es  0, Minitab muestra la gráfica de valores atípicos sin la línea de referencia.
0, Minitab muestra la gráfica de valores atípicos sin la línea de referencia.
Notación
| Término | Description |
|---|---|
| Yi | vector de valor de datos en la fila i |
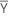 | vector medio |
| S-1 | inversa de la matriz de covarianzas |
| p | el número de variables |
| n | el número de filas presentes |
