En este tema
Paso 1: Determinar el número de componentes principales
- Proporción de la varianza que los componentes explican
- Utilice la proporción acumulada para determinar la cantidad total de varianza que explican los componentes principales. Conserve los componentes principales que explican un nivel aceptable de varianza. El nivel aceptable depende de la aplicación específica. Para propósitos descriptivos, es posible que solo necesite explicar el 80% de la varianza. Sin embargo, si desea realizar otros análisis con los datos, se recomienda que los componentes principales expliquen por lo menos el 90% de la varianza.
- Valores propios
- Usted puede utilizar el tamaño del valor propio para determinar el número de componentes principales. Conserve los componentes principales con los valores propios más grandes. Por ejemplo, según el criterio de Kaiser, se usan solo los componentes principales con valores propios que son mayores que 1.
- Gráfica de sedimentación
- La gráfica de sedimentación ordena los valores propios desde el más grande hasta el más pequeño. El patrón ideal es una curva pronunciada, seguida de una inflexión y luego de una línea recta. Utilice los componentes en la curva pronunciada antes del primer punto que inicia la tendencia de línea.
Análisis de los valores y vectores propios de la matriz de correlación
| Valor propio | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| Proporción | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| Acumulada | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
Vectores propios
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Ingresos | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| Educación | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| Edad | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| Residencia | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| Empleo | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| Ahorros | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| Deuda | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| Tarj Crédito | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
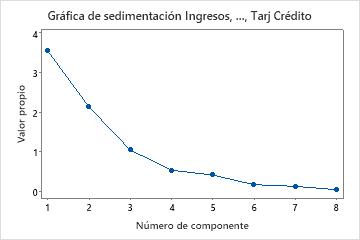
Resultados clave: Acumulada, Valor propio, Gráfica de sedimentación
En estos resultados, los tres primeros componentes principales tienen valores propios mayores que 1. Estos tres componentes explican 84,1% de la variación en los datos. La gráfica de sedimentación muestra que los valores propios comienzan a formar una línea recta después del tercer componente principal. Si 84,1% es una cantidad adecuada de variación explicada en los datos, entonces debe utilizar los tres primeros componentes principales.
Paso 2: Interpretar cada componente principal en términos de las variables originales
Para interpretar cada componente principal, examine la magnitud y la dirección de los coeficientes de las variables originales. Cuanto mayor sea el valor absoluto del coeficiente, más importante será la variable correspondiente en el cálculo del componente. Qué tan grande debe ser el valor absoluto de un coeficiente para ser considerado importante es subjetivo. Utilice su conocimiento especializado para determinar en qué nivel el valor de correlación es importante.
Análisis de los valores y vectores propios de la matriz de correlación
| Valor propio | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| Proporción | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| Acumulada | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
Vectores propios
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Ingresos | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| Educación | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| Edad | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| Residencia | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| Empleo | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| Ahorros | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| Deuda | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| Tarj Crédito | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
Resultados clave: PC, gráfica de influencias
En estos resultados, el primer componente principal tiene asociaciones positivas grandes con Edad, Residencia, Empleo y Ahorros, así que este componente mide principalmente estabilidad financiera a largo plazo. El segundo componente tiene asociaciones negativas grandes con Deudas y Tarj Crédito, así que este componente mide principalmente el historial crediticio de un solicitante. El tercer componente tiene asociaciones negativas grandes con Ingresos, Educación y Tarj Crédito, así que este componente mide principalmente las calificaciones académicas y de ingresos del solicitante.
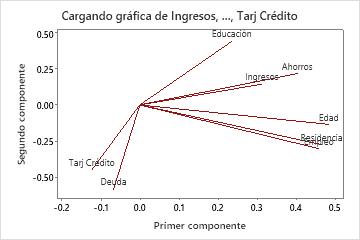
La gráfica de influencias muestra visualmente los resultados de los dos primeros componentes. Edad, Residencia, Empleo y Ahorros tienen influencias positivas grandes en el componente 1, así que este componente mide la estabilidad financiera a largo plazo. Deudas y Tarj Crédito tienen influencias negativas grandes en el componente 2, así que este componente mide principalmente el historial crediticio de un solicitante.
Paso 3: Identificar valores atípicos
Utilice la gráfica de valores atípicos para identificar valores atípicos. Cualquier punto que se encuentre por encima de la línea de referencia es un valor atípico. Los valores atípicos pueden afectar significativamente los resultados de su análisis. Por lo tanto, si identifica un valor atípico en los datos, debe examinar la observación para determinar por qué se trata de un valor poco común. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los datos que estén asociados a causas especiales y repetir el análisis.
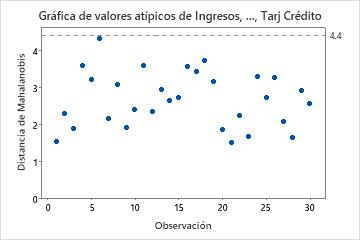
Resultado clave: Gráfica de valores atípicos
En estos resultados, no hay valores atípicos. Todos los puntos están por debajo de la línea de referencia.
Sugerencia
Mantenga el cursor sobre cualquier punto en una gráfica de valores atípicos para identificar la observación. Utilice para destacar múltiples valores atípicos en la gráfica y marcar las observaciones en la hoja de trabajo.
