En este tema
Matriz de correlación
La matriz de correlación muestra los valores de correlación de Pearson, que miden el grado de relación lineal entre cada par de elementos o variables. Los valores de correlación se pueden ubicar entre -1 y +1. Sin embargo, en la práctica, los elementos por lo general tienen correlaciones positivas. Si los dos elementos tienden a aumentar o disminuir al mismo tiempo, el valor de correlación es positivo.
Interpretación
Utilice la matriz de correlación para evaluar la fuerza y dirección de la relación entre dos elementos o variables. Un valor de correlación alto y positivo indica que los elementos miden la misma destreza o característica. Si los elementos no están altamente correlacionados, entonces los elementos pudieran medir diferentes características o no estar claramente definidos.
A menudo, las variables con valores de correlación mayores que 0.7 se consideran altamente correlacionadas. Sin embargo, el valor de referencia adecuado que se utilizará también depende de las normas en su área de estudio y el número de elementos en el análisis.
Matriz de correlación
| Elemento 1 | Elemento 2 | |
|---|---|---|
| Elemento 2 | 0.903 | |
| Elemento 3 | 0.867 | 0.864 |
En estos resultados, todos los elementos están altamente correlacionados entre sí. El Elemento 1 y el Elemento 2 tienen una correlación lineal positiva de 0.903. El Elemento 1 y el Elemento 3 tienen una correlación lineal positiva de 0.867, mientras que el Elemento 2 y el Elemento 3 tienen una correlación lineal positiva de 0.864. Por lo tanto, estos elementos parecen medir la misma característica.
Matriz de covarianzas
La matriz de covarianzas muestra los valores de covarianza, que miden la relación lineal de cada par de elementos o variables. Los valores de covarianza positivos indican que valores por encima del promedio de una variable están asociados con valores por encima del promedio de la otra variable y que valores por debajo del promedio de una variable están asociados con valores por debajo del promedio de la otra variable. Los valores de covarianza negativos indican que valores por encima del promedio de una variable están asociados con valores por debajo del promedio de la otra variable.
A diferencia del coeficiente de correlación, la covarianza no es estandarizada. Por lo tanto, los valores de covarianza pueden encontrarse entre infinito negativo e infinito positivo y puede ser difícil interpretarlos. Para interpretar más fácilmente la relación lineal entre cada par de elementos o variables, utilice la matriz de correlación.
Media
La media es la suma de todas las observaciones dividida entre el número de observaciones. Minitab calcula la media de cada elemento y la media total. La media de un elemento es la suma de todas las puntuaciones de un elemento dividida entre el número de puntuaciones de ese elemento. La media total es la suma de todas las medias de los elementos.
Interpretación
Utilice la media de elemento para describir las puntuaciones de cada elemento o variable con un solo valor que representa el centro de los datos.
Estadísticas totales y de elementos
| Variable | Conteo total | Media | Desv.Est. |
|---|---|---|---|
| Elemento 1 | 50 | 3.1600 | 1.2675 |
| Elemento 2 | 50 | 2.8400 | 1.3607 |
| Elemento 3 | 50 | 2.9400 | 1.3463 |
| Total | 50 | 8.9400 | 3.8087 |
En estos resultados, la puntuación media del Elemento 1 es la mayor (3.16) y la puntuación media del Elemento 2 es la menor (2.84). La media total es la suma de las medias de los tres elementos.
Desv.Est.
La desviación estándar (Desv.Est.) es una medida de dispersión que indica qué tan dispersos están los datos alrededor de la media. Minitab calcula la desviación estándar de las puntuaciones de cada elemento o variable, así como el total de las desviaciones estándar.
Interpretación
Utilice la desviación estándar de los elementos para determinar qué tan dispersas están las puntuaciones con respecto a la media de cada elemento.
Estadísticas totales y de elementos
| Variable | Conteo total | Media | Desv.Est. |
|---|---|---|---|
| Elemento 1 | 50 | 3.1600 | 1.2675 |
| Elemento 2 | 50 | 2.8400 | 1.3607 |
| Elemento 3 | 50 | 2.9400 | 1.3463 |
| Total | 50 | 8.9400 | 3.8087 |
En estos resultados, las puntuaciones del Elemento 2 tienen la mayor desviación estándar (1.3607). Esto indica que las puntuaciones del Elemento 2 tienen la mayor variabilidad de los tres elementos. El Elemento 1 tiene la menor desviación estándar (1.2675) y la menor variabilidad de las puntuaciones. La desviación estándar total es la suma de las desviaciones estándar de los tres elementos.
Alfa de Cronbach
El alfa de Cronbach es una medida de uniformidad interna que se calcula utilizando la varianza de la muestra, las puntuaciones totales y el número de elementos.
Interpretación
Utilice el alfa de Cronbach para examinar el nivel de uniformidad con que múltiples elementos en una encuesta o prueba evalúan la misma destreza o característica. Los valores más altos del alfa de Cronbach sugieren una mayor uniformidad interna. Un valor de referencia comúnmente utilizado es 0.7. Generalmente, si el alfa de Cronbach es mayor que 0.7, entonces usted tiene evidencia de que los elementos de la encuesta o prueba miden la misma destreza o característica. Si el alfa de Cronbach es menor que 0.7, entonces los elementos pudieran no medir de manera confiable una destreza o característica individual para concluir que por lo menos algunos de los elementos miden la misma característica. Sin embargo, el valor de referencia adecuado que se utilizará también depende de las normas en su área de estudio y el número de elementos en el análisis.
Alfa de Cronbach
| Alfa |
|---|
| 0.9550 |
En estos resultados, el alfa de Cronbach general es 0.955. El valor es mayor que el valor de referencia común de 0.7 y sugiere que los elementos miden la misma característica.
Media total ajust.
La media total ajustada es la suma de todas las medias de los elementos, excepto la media del elemento omitido.
Interpretación
Utilice la media total ajustada para ver cómo el valor de la media total cambia cuando se elimina un elemento del análisis.
Estadísticas de elementos omitidas
| Variable omitida | Media total ajustada | Desv.Est. total ajustada | Correlación total ajustada por elemento | Correlación múltiple cuadrada | Alfa de Cronbach |
|---|---|---|---|---|---|
| Elemento 1 | 5.780 | 2.613 | 0.9166 | 0.8447 | 0.9268 |
| Elemento 2 | 6.100 | 2.525 | 0.9134 | 0.8413 | 0.9277 |
| Elemento 3 | 6.000 | 2.563 | 0.8870 | 0.7869 | 0.9476 |
En estos resultados, la media total ajustada cuando se omite el Elemento 1 del análisis es 5.78. Es decir, la suma de la puntuación media del Elemento 2 y la puntuación media del Elemento 3 es 5.78.
Desv.Est. total ajust.
La desviación estándar total ajustada es la desviación estándar de la puntuación total después de omitir un elemento.
Interpretación
Utilice la desviación estándar total ajustada para ver cómo el valor de la desviación estándar total cambia cuando se elimina un elemento del análisis.
Estadísticas de elementos omitidas
| Variable omitida | Media total ajustada | Desv.Est. total ajustada | Correlación total ajustada por elemento | Correlación múltiple cuadrada | Alfa de Cronbach |
|---|---|---|---|---|---|
| Elemento 1 | 5.780 | 2.613 | 0.9166 | 0.8447 | 0.9268 |
| Elemento 2 | 6.100 | 2.525 | 0.9134 | 0.8413 | 0.9277 |
| Elemento 3 | 6.000 | 2.563 | 0.8870 | 0.7869 | 0.9476 |
En estos resultados, la desviación estándar ajustada cuando se omite el Elemento 1 del análisis es 2.613.
Corr. total ajustada de elemento
La correlación total ajustada de elemento es la correlación entre las puntuaciones de un elemento omitido y las puntuaciones totales de todos los demás elementos. Aunque los valores de la correlación total ajustada de elemento puede en teoría variar de -1 a 1, en la práctica los valores usualmente varían entre 0 y 1.
Interpretación
Utilice la correlación total ajustada de elemento para evaluar si la eliminación de un elemento del análisis mejora la uniformidad interna. Un valor más alto de correlación ajustada de elemento (más cerca de 1) sugiere que el elemento omitido mide la misma característica que los demás elementos. Si un elemento omitido tiene un valor bajo de correlación ajustada de elemento, un valor bajo de correlación múltiple cuadrada y un valor substancialmente más alto del alfa de Cronbach, entonces usted pudiera considerar eliminar el elemento de la encuesta o prueba para mejorar su uniformidad interna.
Estadísticas de elementos omitidas
| Variable omitida | Media total ajustada | Desv.Est. total ajustada | Correlación total ajustada por elemento | Correlación múltiple cuadrada | Alfa de Cronbach |
|---|---|---|---|---|---|
| Elemento 1 | 5.780 | 2.613 | 0.9166 | 0.8447 | 0.9268 |
| Elemento 2 | 6.100 | 2.525 | 0.9134 | 0.8413 | 0.9277 |
| Elemento 3 | 6.000 | 2.563 | 0.8870 | 0.7869 | 0.9476 |
En estos resultados, la correlación total ajustada de elemento para el Elemento 1 es 0.9166. La correlación total ajustada de elemento para el Elemento 2 es 0.9134. La correlación total ajusta de elemento para el Elemento 3 es 0.887. Debido a que la correlación total ajustada de elemento para todos los elementos omitidos es uniformemente alta, la evidencia sugiere que todos los elementos miden la misma característica.
Correlación múltiple cuadrada
La correlación múltiple cuadrada es el coeficiente de determinación (R2) cuando se aplica una regresión al elemento omitido en los elementos restantes. Los valores varían entre 0 y 1.
Interpretación
Utilice los valores de correlación múltiple cuadrada para evaluar si la eliminación de un elemento del análisis mejora la uniformidad interna. Un valor más alto de correlación múltiple cuadrada (más cerca de 1) sugiere que el elemento omitido mide la misma característica que los demás elementos. Si un elemento omitido tiene un valor bajo de correlación múltiple cuadrada, un valor bajo de correlación total ajustada de elemento y un valor substancialmente más alto del alfa de Cronbach, entonces usted pudiera considerar eliminar el elemento de la encuesta o prueba para mejorar su uniformidad interna.
Estadísticas de elementos omitidas
| Variable omitida | Media total ajustada | Desv.Est. total ajustada | Correlación total ajustada por elemento | Correlación múltiple cuadrada | Alfa de Cronbach |
|---|---|---|---|---|---|
| Elemento 1 | 5.780 | 2.613 | 0.9166 | 0.8447 | 0.9268 |
| Elemento 2 | 6.100 | 2.525 | 0.9134 | 0.8413 | 0.9277 |
| Elemento 3 | 6.000 | 2.563 | 0.8870 | 0.7869 | 0.9476 |
En estos resultados, la correlación múltiple cuadrada para el Elemento 1 es 0.8447. La correlación múltiple cuadrada para el Elemento 2 es 0.8413. La correlación múltiple cuadrada para el Elemento 3 es 0.7869. Debido a que la correlación múltiple cuadrada de todos los elementos omitidos es uniformemente alta, la evidencia sugiere que todos los elementos miden la misma característica.
Alfa de Cronbach (para un elemento omitido)
El alfa de Cronbach para un elemento omitido es el valor del alfa de Cronbach para los elementos restantes después que un elemento se elimina del análisis. El alfa de Cronbach es una medida de uniformidad interna que se calcula utilizando la varianza de la muestra, las puntuaciones totales y el número de elementos.
Interpretación
Utilice el alfa de Cronbach para elementos omitidos para evaluar si la eliminación de un elemento del análisis mejora la uniformidad interna. Valores altamente uniformes del alfa de Cronbach para todos los elementos omitidos sugieren que todos los elementos miden la misma característica. Un alfa de Cronbach substancialmente más alto para un elemento omitido específico sugiere que pudiera no medir la misma característica que los demás elementos. Si un elemento omitido tiene un valor bajo de correlación múltiple cuadrada, un valor bajo de correlación total ajustada de elemento y un valor substancialmente más alto del alfa de Cronbach, entonces usted pudiera considerar eliminar el elemento de la encuesta o prueba para mejorar su uniformidad interna.
Estadísticas de elementos omitidas
| Variable omitida | Media total ajustada | Desv.Est. total ajustada | Correlación total ajustada por elemento | Correlación múltiple cuadrada | Alfa de Cronbach |
|---|---|---|---|---|---|
| Elemento 1 | 5.780 | 2.613 | 0.9166 | 0.8447 | 0.9268 |
| Elemento 2 | 6.100 | 2.525 | 0.9134 | 0.8413 | 0.9277 |
| Elemento 3 | 6.000 | 2.563 | 0.8870 | 0.7869 | 0.9476 |
En estos resultados, el alfa de Cronbach cuando se omite el elemento 1 es 0.9268. El alfa de Cronbach cuando se omite el elemento 2 es 0.9277. El alfa de Cronbach cuando se omite el elemento 3 es 0.9476. Debido a que el alfa de Cronbach para todos los elementos omitidos es similar, la evidencia sugiere que todos los elementos miden la misma característica.
Gráfica de matriz
Una gráfica de matriz es un arreglo de gráficas de dispersión. Cada gráfica de dispersión en la matriz grafica las puntuaciones de un par de elementos en los ejes X y Y.
Interpretación
Utilice la gráfica para evaluar visualmente la relación entre cada combinación de elementos o variables.
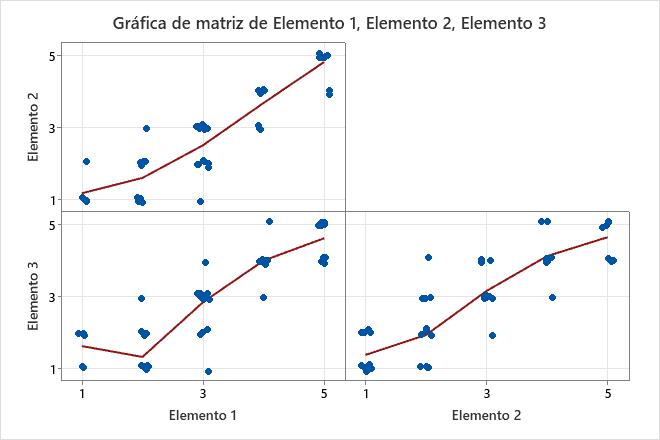
Esta gráfica de matriz sugiere que todos los pares de elementos tienen una relación lineal positiva.
