En este tema
Influencias de los factores
Las influencias de los factores indican cuánto explica un factor a una variable. Las influencias pueden ir de -1 a 1.
Minitab calcula las influencias de los factores no rotadas y las influencias de los factores rotadas si usted selecciona un método de rotación para el análisis.
Interpretación
Examine el patrón de influencias para determinar el factor que ejerce mayor influencia en cada variable. Las influencias cercanas a -1 o 1 indican que el factor afecta considerablemente a la variable. Las influencias cercanas a 0 indican que el factor tiene poca influencia en la variable. Algunas variables pueden tener grandes influencias sobre múltiples factores.
Las influencias de factores no rotadas a menudo son difíciles de interpretar. La rotación de factores simplifica la estructura de influencias y frecuentemente hace que los factores se distingan más claramente y sean más fáciles de interpretar. Sin embargo, un método de rotación pudiera no ser el más adecuado en todos los casos. Se recomienda intentar con diferentes rotaciones y utilizar la que produzca los resultados más apropiados. Usted también puede ordenar las influencias rotadas para evaluar más claramente las influencias dentro de un factor.
- Aptitud para la compañía (0.778), Aptitud para el empleo (0.844) y Potencial (0.645) tienen influencias positivas grandes en el factor 1, así que este factor describe la aptitud y potencial del empleado para crecer en la compañía.
- Apariencia (0.730), Simpatía (0.615) y Autoconfianza (0.743) tienen influencias positivas grandes en el factor 2, así que este factor describe las cualidades personales.
- Comunicación (0.802) y Organización (0.889) tienen influencias positivas grandes en el factor 3, así que este factor describe destrezas para el trabajo.
- Carta (0.947) y C. V. (0.789) tienen influencias positivas grandes en el factor 4, así que este factor describe destrezas para la redacción.
Cargas de factores no rotados y comunalidades
| Variable | Factor1 | Factor2 | Factor3 | Factor4 | Comunalidad |
|---|---|---|---|---|---|
| Estudios | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| Apariencia | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| Comunicación | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| Apto P Cía | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| Experiencia | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| Apto P Trabajo | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| Carta | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| Simpatía | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| Organización | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| Potencial | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| C. V. | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| Autoconfianza | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| Varianza | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % Var | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
Cargas de factores rotados y comunalidades
| Variable | Factor1 | Factor2 | Factor3 | Factor4 | Comunalidad |
|---|---|---|---|---|---|
| Estudios | 0.481 | 0.510 | 0.086 | 0.188 | 0.534 |
| Apariencia | 0.140 | 0.730 | 0.319 | 0.175 | 0.685 |
| Comunicación | 0.203 | 0.280 | 0.802 | 0.181 | 0.795 |
| Apto P Cía | 0.778 | 0.165 | 0.445 | 0.189 | 0.866 |
| Experiencia | 0.472 | 0.395 | -0.112 | 0.401 | 0.553 |
| Apto P Trabajo | 0.844 | 0.209 | 0.305 | 0.215 | 0.895 |
| Carta | 0.219 | 0.052 | 0.217 | 0.947 | 0.994 |
| Simpatía | 0.261 | 0.615 | 0.321 | 0.208 | 0.593 |
| Organización | 0.217 | 0.285 | 0.889 | 0.086 | 0.926 |
| Potencial | 0.645 | 0.492 | 0.121 | 0.202 | 0.714 |
| C. V. | 0.214 | 0.365 | 0.113 | 0.789 | 0.814 |
| Autoconfianza | 0.239 | 0.743 | 0.249 | 0.092 | 0.679 |
| Varianza | 2.5153 | 2.4880 | 2.0863 | 1.9594 | 9.0491 |
| % Var | 0.210 | 0.207 | 0.174 | 0.163 | 0.754 |
Comunalidad
La comunalidad es la proporción de variabilidad de cada variable que es explicada por los factores. El valor de comunalidad es el mismo, independientemente de si utiliza las influencias de los factores no rotadas o las influencias de los factores rotadas para el análisis.
Interpretación
Examine los valores de comunalidad para evaluar en qué grado los factores explican cada variable. Mientras más cerca de 1 esté la comunalidad, mejor explicarán los factores la variable. Usted puede decidir agregar un factor si este contribuye significativamente al ajuste de ciertas variables.
Cargas de factores no rotados y comunalidades
| Variable | Factor1 | Factor2 | Factor3 | Factor4 | Comunalidad |
|---|---|---|---|---|---|
| Estudios | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| Apariencia | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| Comunicación | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| Apto P Cía | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| Experiencia | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| Apto P Trabajo | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| Carta | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| Simpatía | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| Organización | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| Potencial | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| C. V. | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| Autoconfianza | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| Varianza | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % Var | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
En estos resultados, se extrajeron 4 factores de las 12 variables. Sus valores de comunalidad son generalmente altos para todas las variables, lo cual indica que los 4 factores representan adecuadamente las variables. Por ejemplo, los 4 factores explican 0.895, o 89.5%, de la variabilidad en Aptitud para el empleo.
Varianza
La variabilidad en los datos explicada por cada factor. Si usted utiliza el método de extracción de componentes principales y no rota las influencias, la varianza de cada factor es igual a su valor propio. La rotación cambia la distribución de la proporción de variación explicada por cada factor, aunque la variación total explicada por todos los factores se mantiene igual.
Interpretación
Examine la varianza de cada factor. Cuanto mayor sea la varianza, en mayor cantidad explicará ese factor la variabilidad en los datos. Si usted no sabe cuántos factores extraer en el análisis, puede utilizar primero el método de extracción de componentes principales, sin rotación, usando el número predeterminado de factores (que extrae el número máximo de factores) como una evaluación preliminar. Luego defina los factores importantes como los que tienen una varianza (valor propio) mayor que cierto valor. Por ejemplo, un criterio es incluir cualquier factor con un valor propio de por lo menos 1. Otro método es evaluar visualmente los valores propios en la gráfica de sedimentación para determinar en qué punto los valores propios muestran poco cambio y se acercan a 0. Para obtener más información, vea el tema sobre Gráfica de sedimentación.
Cargas de factores no rotados y comunalidades
| Variable | Factor1 | Factor2 | Factor3 | Factor4 | Factor5 | Factor6 | Factor7 | Factor8 |
|---|---|---|---|---|---|---|---|---|
| Estudios | 0.726 | 0.336 | -0.326 | 0.104 | -0.354 | -0.099 | 0.233 | 0.147 |
| Apariencia | 0.719 | -0.271 | -0.163 | -0.400 | -0.148 | -0.362 | -0.195 | -0.151 |
| Comunicación | 0.712 | -0.446 | 0.255 | 0.229 | -0.319 | 0.119 | 0.032 | 0.088 |
| Apto P Cía | 0.802 | -0.060 | 0.048 | 0.428 | 0.306 | -0.137 | -0.067 | 0.105 |
| Experiencia | 0.644 | 0.605 | -0.182 | -0.037 | -0.092 | 0.317 | -0.209 | -0.102 |
| Apto P Trabajo | 0.813 | 0.078 | -0.029 | 0.365 | 0.368 | -0.067 | -0.025 | -0.032 |
| Carta | 0.625 | 0.327 | 0.654 | -0.134 | 0.031 | 0.025 | 0.017 | -0.113 |
| Simpatía | 0.739 | -0.295 | -0.117 | -0.346 | 0.249 | 0.140 | 0.353 | -0.142 |
| Organización | 0.706 | -0.540 | 0.140 | 0.247 | -0.217 | 0.136 | -0.080 | -0.105 |
| Potencial | 0.814 | 0.290 | -0.326 | 0.167 | -0.068 | -0.073 | 0.048 | -0.112 |
| C. V. | 0.709 | 0.298 | 0.465 | -0.343 | -0.022 | -0.107 | 0.024 | 0.170 |
| Autoconfianza | 0.719 | -0.262 | -0.294 | -0.409 | 0.175 | 0.179 | -0.159 | 0.230 |
| Varianza | 6.3876 | 1.4885 | 1.1045 | 1.0516 | 0.6325 | 0.3670 | 0.3016 | 0.2129 |
| % Var | 0.532 | 0.124 | 0.092 | 0.088 | 0.053 | 0.031 | 0.025 | 0.018 |
| Variable | Factor9 | Factor10 | Factor11 | Factor12 | Comunalidad |
|---|---|---|---|---|---|
| Estudios | 0.097 | -0.142 | -0.026 | -0.031 | 1.000 |
| Apariencia | 0.082 | 0.016 | 0.020 | -0.038 | 1.000 |
| Comunicación | 0.023 | 0.204 | 0.012 | -0.100 | 1.000 |
| Apto P Cía | -0.019 | -0.067 | 0.188 | -0.021 | 1.000 |
| Experiencia | 0.121 | 0.039 | 0.077 | 0.009 | 1.000 |
| Apto P Trabajo | 0.146 | 0.066 | -0.176 | 0.008 | 1.000 |
| Carta | -0.079 | -0.130 | -0.043 | -0.127 | 1.000 |
| Simpatía | 0.051 | 0.022 | 0.064 | 0.012 | 1.000 |
| Organización | -0.020 | -0.162 | -0.032 | 0.136 | 1.000 |
| Potencial | -0.290 | 0.100 | -0.023 | 0.028 | 1.000 |
| C. V. | 0.008 | 0.090 | 0.010 | 0.156 | 1.000 |
| Autoconfianza | -0.098 | -0.061 | -0.065 | -0.047 | 1.000 |
| Varianza | 0.1557 | 0.1379 | 0.0851 | 0.0750 | 12.0000 |
| % Var | 0.013 | 0.011 | 0.007 | 0.006 | 1.000 |
Este análisis se realizó utilizando el método de componentes principales y la configuración predeterminada (sin rotación). Los cuatro primeros factores tienen varianza (valores propios) mayor que 1. Los valores propios cambian menos marcadamente cuando se utilizan más de 6 factores. Por lo tanto, 4 factores explican la mayor parte de la variabilidad en los datos. Con base en estos resultados preliminares, repita el análisis factorial y extraiga solo 4 factores, además de experimentar con diferentes rotaciones.
% Var
El porcentaje de varianza (%Var) es la proporción de variabilidad en los datos explicada por cada factor. Los valores de % Var pueden ir de 0 (0%) a 1 (100%).
Interpretación
Examine el valor de % Var de cada factor. Valores más altos de % Var indican que un factor explica una mayor parte de la variabilidad. Por lo tanto, usted puede utilizar los valores de % Var para determinar cuáles factores son más importantes.
El valor de comunalidad de % Var indica la variación total explicada por todos los factores en el análisis. Utilice este valor para ayudar a determinar si el número de factores usado en el análisis explica una cantidad suficiente de variación total en los datos.
Cargas de factores no rotados y comunalidades
| Variable | Factor1 | Factor2 | Factor3 | Factor4 | Comunalidad |
|---|---|---|---|---|---|
| Estudios | 0.380 | 0.455 | 0.340 | 0.259 | 0.534 |
| Apariencia | 0.359 | 0.530 | -0.040 | 0.523 | 0.685 |
| Comunicación | 0.465 | 0.660 | -0.377 | -0.023 | 0.795 |
| Apto P Cía | 0.523 | 0.677 | 0.266 | -0.253 | 0.866 |
| Experiencia | 0.508 | 0.194 | 0.450 | 0.232 | 0.553 |
| Apto P Trabajo | 0.532 | 0.632 | 0.415 | -0.201 | 0.895 |
| Carta | 0.992 | -0.094 | -0.012 | -0.007 | 0.994 |
| Simpatía | 0.412 | 0.529 | 0.032 | 0.377 | 0.593 |
| Organización | 0.406 | 0.761 | -0.424 | -0.055 | 0.926 |
| Potencial | 0.446 | 0.548 | 0.431 | 0.172 | 0.714 |
| C. V. | 0.850 | 0.040 | 0.096 | 0.283 | 0.814 |
| Autoconfianza | 0.293 | 0.575 | 0.083 | 0.506 | 0.679 |
| Varianza | 3.6320 | 3.3193 | 1.0883 | 1.0095 | 9.0491 |
| % Var | 0.303 | 0.277 | 0.091 | 0.084 | 0.754 |
En estos resultados, el Factor 1 explica 0.303, o 30.3%, de la variabilidad en los datos. Los cuatro factores en conjunto explican 0.754, o 75.4%, de la variabilidad en los datos.
Coeficientes de puntuación de los factores
Los coeficientes de los factores identifican la ponderación relativa de cada variable en el componente en un análisis factorial. Cuanto mayor sea el valor absoluto del coeficiente, más importante será la variable correspondiente en el cálculo del componente. Minitab utiliza los coeficientes de los factores para calcular las puntuaciones de los factores, que son los valores estimados de los factores. Minitab calcula las puntuaciones de los factores multiplicando los coeficientes de las puntuaciones de los factores (indicados en Factor 1, Factor 2, y así sucesivamente) y sus datos después de que se han ajustado y centrado al sustraer la medias.
Interpretación
- Examinar el comportamiento de las observaciones.
- Utilizar en otros análisis, tales como regresión o MANOVA.
Nota
Usted debe estandarizar las variables para utilizar los coeficientes estimados para calcular las puntuaciones de los factores.
Gráfica de sedimentación
La gráfica de sedimentación muestra el número del factor versus su valor propio correspondiente. La gráfica de sedimentación ordena los valores propios desde el más grande hasta el más pequeño. Cuando no se ha realizado rotación, los valores propios de la matriz de correlación son iguales a las varianzas de los factores.
Para mostrar la gráfica de sedimentación, usted debe hacer clic en Gráficas y seleccionar la gráfica de sedimentación cuando realiza el análisis.
Interpretación
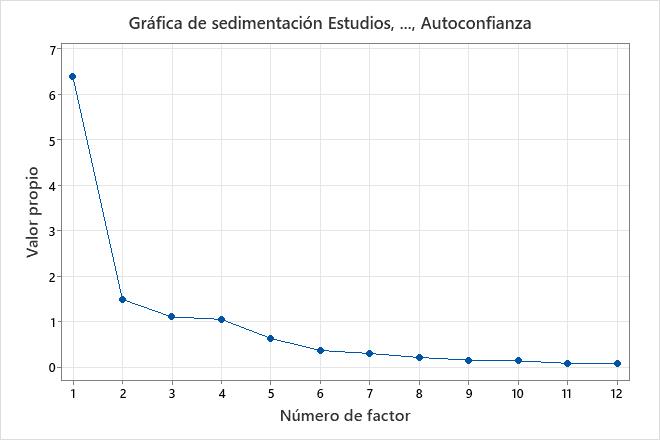
Esta gráfica de sedimentación muestra que los cuatros primeros factores explican la mayor parte de la variabilidad total en los datos (dada por los valores propios). Los valores propios de los cuatro primeros factores son todos mayores que 1. Los factores restantes explican una proporción muy pequeña de la variabilidad y probablemente no son importantes.
Gráfica de puntuaciones
La gráfica de puntuaciones representa las puntuaciones del segundo factor versus las puntuaciones del primer factor.
Para mostrar la gráfica de puntuaciones, usted debe hacer clic en Gráficas y seleccionar la gráfica de puntuaciones cuando realiza el análisis.
Interpretación
Si los dos primeros factores explican la mayor parte de la varianza en los datos, usted puede utilizar la gráfica de puntuaciones para evaluar la estructura de los datos y detectar los conglomerados, los valores atípicos y las tendencias. Agrupaciones de datos en la gráfica pudieran indicar dos o más distribuciones separadas en los datos. Si los datos siguen una distribución normal y no hay valores atípicos presentes, los puntos están distribuidos aleatoriamente alrededor del valor de 0.
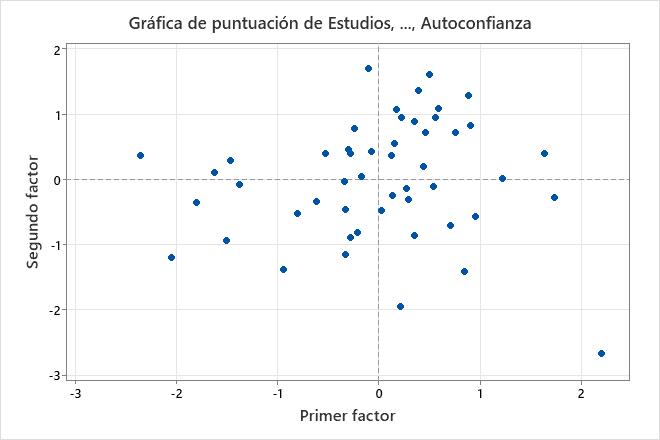
En esta gráfica de puntuaciones, los datos parecen normales y no se observan valores atípicos extremos. Sin embargo, le convendría investigar el valor de datos mostrado en la parte inferior derecha de la gráfica, que se encuentra lejos de los demás valores de datos.
Sugerencia
Para ver la puntuación calculada de cada observación, detenga el cursor en un punto de datos en la gráfica. Para crear gráficas de puntuaciones para otros factores, almacene las puntuaciones y utilice .
Gráfica de influencias
La gráfica de influencias grafica las influencias de los factores rotadas de cada variable para el primer factor versus las influencias de los factores rotadas para el segundo factor.
Para mostrar la gráfica de influencias, usted debe hacer clic en Gráficas y seleccionar la gráfica de influencias cuando realiza el análisis.
Interpretación
Utilice la gráfica influencias para identificar cuáles variables tienen el mayor efecto en los factores. Las influencias pueden ir de -1 a 1. Las influencias que se aproximan a -1 o 1 indican que la variable afecta considerablemente al factor. Las influencias cercanas a 0 indican que la variable tiene poca influencia en el factor. Evaluar las influencias también puede ayudarle a caracterizar cada factor en términos de las variables. Después de seleccionar el número de factores, intente con diferentes rotaciones de manera que pueda interpretar con más facilidad las influencias de los factores.
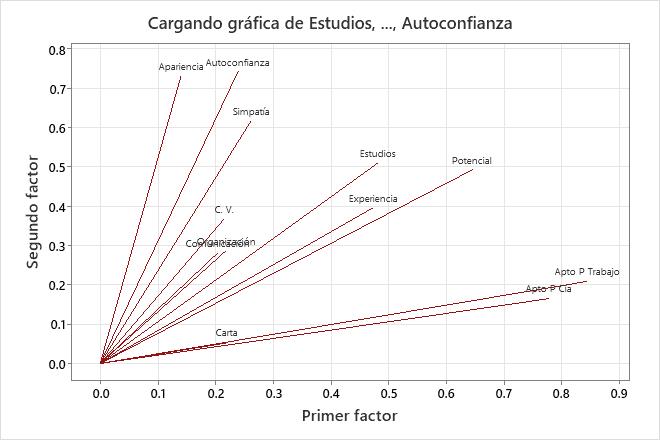
Para esta gráfica de influencias, se realizó una rotación varimax en los datos, lo cual hace que los dos primeros factores se interpreten con más facilidad. Aptitud para el empleo y Aptitud para la compañía tienen influencias positivas grandes en el factor 1, así que este factor describe la idoneidad del solicitante para el cargo. Apariencia, Simpatía y Autoconfianza tienen influencias positivas grandes en el factor 2, así que este factor describe las cualidades personales de un solicitante.
Gráfica de doble proyección
La gráfica de doble proyección sobrepone la gráfica de puntuaciones y la gráfica de influencias.
Para mostrar la gráfica de doble proyección, usted debe hacer clic en Gráficas y seleccionar la gráfica de doble proyección cuando realiza el análisis.
Interpretación
Utilice la gráfica de doble proyección para evaluar la estructura de los datos y las influencias de los dos primeros factores en una gráfica. Minitab grafica las puntuaciones del segundo factor versus las puntuaciones del primer factor, así como las influencias de ambos factores.
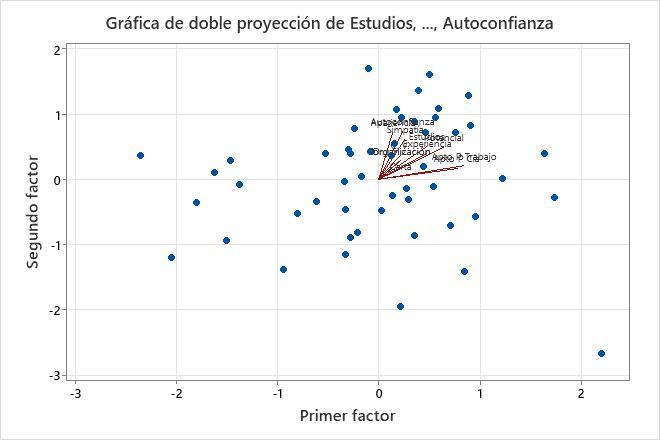
- Los datos parecen normales y no se observan valores atípicos extremos. Sin embargo, se recomienda investigar el valor de datos mostrado en la parte inferior derecha de la gráfica, que se encuentra lejos de los demás valores de datos.
- Aptitud para el empleo y Aptitud para la compañía tienen influencias positivas grandes en el factor 1, así que este factor describe la idoneidad del solicitante para el cargo.
- Apariencia, Simpatía y Autoconfianza tienen influencias positivas grandes en el factor 2, así que este factor describe las cualidades personales de un solicitante.
