En este tema
Paso 1: Identificar el mejor nivel para cada factor de control
Utilice la relación de señal a ruido (relación S/N) para identificar la configuración de factores de control que minimice la variabilidad causada por los factores de ruido. Minitab calcula la relación S/N para cada combinación de factores de control y luego calcula la relación S/N promedio para cada nivel de cada factor de control. Elija entre cuatro relaciones S/N con base en el resultado deseado del proceso. Para obtener más información, vaya a ¿Qué es la relación de señal a ruido en un diseño de Taguchi?.
Delta es la diferencia entre los valores de respuesta más altos y más bajos para cada factor. Minitab asigna los rangos con base en los valores de Delta; el Rango 1 para el valor de Delta más alto, el Rango 2 para el segundo más alto, y así sucesivamente, para indicar el efecto relativo de cada factor en la respuesta.
Tabla de respuesta para relaciones de señal a ruido
| Nivel | Variedad | Luz | Fertilizante | Agua | Riego |
|---|---|---|---|---|---|
| 1 | -1.9266 | -0.6911 | -4.1399 | -0.9870 | 0.2274 |
| 2 | 2.8068 | 1.5712 | 5.0201 | 1.8672 | 0.6527 |
| Delta | 4.7333 | 2.2623 | 9.1600 | 2.8542 | 0.4253 |
| Clasificar | 2 | 4 | 1 | 3 | 5 |
Tabla de respuesta para pendientes
| Nivel | Variedad | Luz | Fertilizante | Agua | Riego |
|---|---|---|---|---|---|
| 1 | 0.6867 | 0.6043 | 0.5264 | 0.5437 | 0.7067 |
| 2 | 0.7440 | 0.8264 | 0.9043 | 0.8870 | 0.7240 |
| Delta | 0.0572 | 0.2220 | 0.3778 | 0.3433 | 0.0174 |
| Clasificar | 4 | 3 | 1 | 2 | 5 |
Tabla de respuesta para desviaciones estándar
| Nivel | Variedad | Luz | Fertilizante | Agua | Riego |
|---|---|---|---|---|---|
| 1 | 0.7794 | 0.5450 | 0.7677 | 0.5222 | 0.6207 |
| 2 | 0.5042 | 0.7387 | 0.5159 | 0.7614 | 0.6629 |
| Delta | 0.2752 | 0.1937 | 0.2518 | 0.2392 | 0.0422 |
| Clasificar | 1 | 4 | 2 | 3 | 5 |
Resultados clave: Delta, Rango
- Fertilizante (Delta 9.1600, Rango = 1) tiene el mayor efecto en la relación S/N, seguido por Variedad (Delta 4.7333, Rango = 2), luego seguido por Agua, Luz y Rocío.
- Fertilizante (Delta 0.3778, Rango = 1) también tiene el mayor efecto en las pendientes, seguido por Agua (Delta 0.3433, Rango = 2), luego seguido por Luz, Variedad y Rocío.
- Variedad (Delta 0.2752, Rango = 1) tiene el mayor efecto en las desviaciones estándar, seguida por Fertilizante (Delta 0.2518, Rango = 2), luego seguido por Agua, Luz y Rocío.
Nota
Si tiene un diseño estático y no tiene un factor de señal, tendrá una tabla de respuesta para medias en lugar de pendientes.
Paso 2: Determinar cuáles factores tienen efectos estadísticamente significativos en la respuesta
- Valor p ≤ α: La asociación es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que hay una asociación estadísticamente significativa entre la variable de respuesta y el término.
- Valor p > α: La asociación no es estadísticamente significativa
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que existe una asociación estadísticamente significativa entre la variable de respuesta y el término. Le convendría reajustar el modelo sin el término.
- Si un coeficiente de un factor es estadísticamente significativo, usted puede concluir que no todas las medias de nivel son iguales.
- Si un coeficiente de un término de interacción es significativo, la relación entre un factor y la respuesta depende del resto de los factores en el término. En este caso, usted no debe interpretar los efectos principales sin considerar el efecto de interacción.
Si un término del modelo no es estadísticamente significativo, puede eliminarlo y volver a ajustar el modelo. Frecuentemente, se utiliza un nivel de significancia de 0,10 para evaluar los términos en un modelo.
El coeficiente describe el tamaño y la dirección de la relación entre un término incluido en el modelo y la variable de respuesta. El valor absoluto del coeficiente indica la fuerza relativa de cada factor.El número de coeficientes que Minitab calcula para un factor es el número de niveles menos uno. Si un factor tiene 3 niveles, Minitab provee 2 coeficientes, los cuales corresponden a los niveles de factor 1 y 2. Si un factor tiene 2 niveles, Minitab provee 1 coeficiente, el cual corresponde al nivel de factor 1. Minitab incluye los valores o el texto que corresponden al nivel.
Las tablas de respuesta muestran el promedio de cada característica de respuesta para cada nivel de cada factor. Las tablas incluyen rangos basados en estadísticos Delta, los cuales comparan la magnitud relativa de los efectos. El estadístico Delta es el mayor menos el menor promedio para cada factor. Minitab asigna rangos basados en los valores de Delta; el rango 1 para el valor de Delta más alto, el rango 2 para el segundo más alto, y así sucesivamente. Utilice los promedios de nivel en las tablas de respuesta para determinar cuál nivel de cada factor provee el mejor resultado.
Coeficientes de modelos estimados para Relaciones SN
| Término | Coef | EE del coef. | T | P |
|---|---|---|---|---|
| Constante | 0.4401 | 0.2384 | 1.846 | 0.316 |
| Variedad 1 | -2.3667 | 0.2384 | -9.926 | 0.064 |
| Luz 1 | -1.1312 | 0.2384 | -4.744 | 0.132 |
| Fertiliz 1 | -4.5800 | 0.2384 | -19.209 | 0.033 |
| Agua 1 | -1.4271 | 0.2384 | -5.985 | 0.105 |
| Riego 1 | -0.2127 | 0.2384 | -0.892 | 0.536 |
| Variedad*Fertiliz 1 1 | -0.6041 | 0.2384 | -2.534 | 0.239 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 0.6744 | 99.81% | 98.69% |
Análisis de Varianza de Relaciones SN
| Fuente | GL | SC Sec. | SC Ajust. | MC Ajust. | F | P |
|---|---|---|---|---|---|---|
| Variedad | 1 | 44.809 | 44.809 | 44.809 | 98.52 | 0.064 |
| Luz | 1 | 10.236 | 10.236 | 10.236 | 22.51 | 0.132 |
| Fertilizante | 1 | 167.811 | 167.811 | 167.811 | 368.97 | 0.033 |
| Agua | 1 | 16.293 | 16.293 | 16.293 | 35.82 | 0.105 |
| Riego | 1 | 0.362 | 0.362 | 0.362 | 0.80 | 0.536 |
| Variedad*Fertilizante | 1 | 2.920 | 2.920 | 2.920 | 6.42 | 0.239 |
| Error residual | 1 | 0.455 | 0.455 | 0.455 | ||
| Total | 7 | 242.886 |
Resultados clave: Valor p, coeficientes
En este ejemplo, para la relación de señal a ruido, Fertilizante tiene un valor p que es menor que 0,05, por lo que Fertilizante es estadísticamente significativo en un nivel de significancia de 0,05.
Paso 3: Examinar gráficamente los efectos de los factores
Nota
Aunque se pueden utilizar estas gráficas para mostrar los efectos, asegúrese de evaluar la significancia estadística de los efectos en el análisis que se ajusta al modelo. Si los efectos de interacción son estadísticamente significativos en ese análisis, usted no puede interpretar los efectos principales sin considerar los efectos de interacción.
Gráfica de efectos principales
Las gráficas de efectos principales muestran cómo cada factor afecta la característica de respuesta (relación S/N, medias, pendientes, desviaciones estándar). Existe un efecto principal cuando diferentes niveles de un factor afectan la característica de manera diferente. En el caso de un factor con dos niveles, usted puede descubrir que un nivel aumenta la media en comparación con el otro. Esta diferencia es un efecto principal.
- Cuando la línea es horizontal, entonces no hay un efecto principal. Cada nivel del factor afecta la característica de la misma manera y el promedio de la característica es igual para todos los niveles de factor.
- Cuando la línea no es horizontal, entonces hay un efecto principal. Los diferentes niveles del factor afectan la característica de manera diferente. Mientras mayor sea la diferencia en la posición vertical de los puntos graficados (menos paralela al eje X esté la línea), mayor será la magnitud del efecto principal.
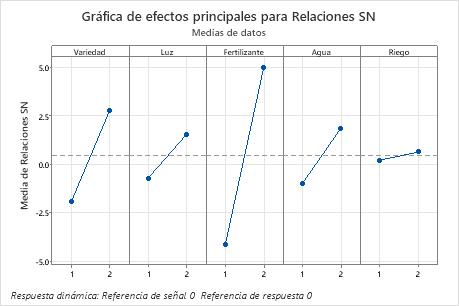
En estos resultados, la gráfica de efectos principales para relación S/N indica que Fertilizante ejerce el mayor efecto en la relación de señal a ruido. En promedio, las corridas experimentales con el Fertilizante 2 registraron relaciones de señal a ruido más altas que las corridas experimentales con el Fertilizante 1. El rocío tuvo poco o ningún efecto en la relación de señal a ruido.
Gráfica de interacción
- Si las líneas son paralelas entres sí, entonces no hay interacción entre los dos factores.
- Si las líneas no son paralelas entre sí, entonces existe interacción entre los dos factores.
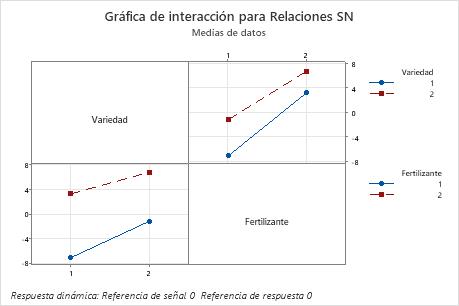
En estos resultados, para las relaciones S/N, las líneas se acercan a paralelas. La Variedad 2 tiene una relación S/N más alta que la Variedad 1 utilizando tanto el Fertilizante 1 como el 2.
Además de las gráficas de interacción, examine el análisis de modelo lineal para determinar si la interacción es significativa.
Gráfica de dispersión
- La línea de regresión de mínimos cuadrados a través del punto de referencia.
- El número de fila en la parte superior de cada gráfica, que hace referencia a la primera fila en la cual aparece la configuración de factores para esa gráfica.
- La relación de señal a ruido, la pendiente y la desviación estándar correspondientes a la configuración de factores, que están ubicadas en la parte inferior de la gráfica.
Las gráficas están organizadas en orden decreciente de la relación de señal a ruido, de modo que las corridas experimentales con las relaciones más altas se grafican primero. Si el experimento tiene más de nueve combinaciones de valores de configuración de factores, Minitab muestra más de una gráfica de dispersión.
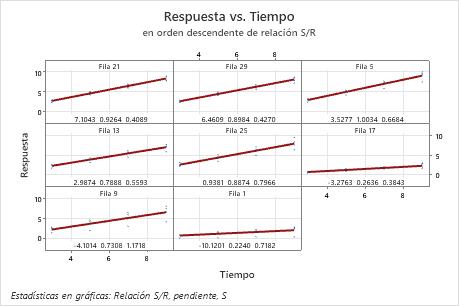
En esta gráfica, existe una diferencia sustancial en la dispersión de los datos entre el mejor y el peor ajuste. Por ejemplo, en la gráfica de la primera celda, para la fila 21, los datos están muy cercanos a la línea. En la gráfica de la esquina inferior izquierda, para la fila 9, los datos varían de una forma mucho más amplia. La desviación estándar para la fila 21 es 0,4089, pero es mucho más en la fila 9. La desviación estándar en la fila 9 es 1,1718.
Paso 4: Determinar si el modelo cumple con los supuestos del análisis
Utilice las gráficas de residuos como ayuda para determinar si el modelo es adecuado y cumple con los supuestos del análisis. Si los supuestos no se cumplen, el modelo podría no ajustarse a los datos adecuadamente y se debería tener cuidado al interpretar los resultados.
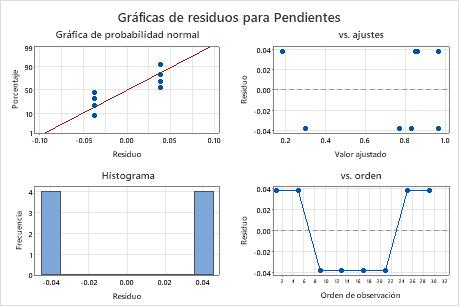
En estos resultados, las gráficas de residuos muestran que solo hay un grado de libertad para error y solo dos valores distintos de los residuos. Es probable que el modelo esté sobreajustado, con demasiados términos. En tal caso, considere reducir el modelo y volver a examinar las gráficas de residuos.
Gráfica de probabilidad normal de los residuos
Utilice la gráfica de probabilidad normal de los residuos para comprobar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
Los patrones que se observan en la siguiente tabla podrían indicar que el modelo no cumple con los supuestos del modelo.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| No una línea recta | No normalidad |
| Un punto que está alejado de la línea | Un valor atípico |
| Cambio en la pendiente | Una variable no identificada |
Gráfica de residuos vs. ajustes
Los patrones que se observan en la siguiente tabla podrían indicar que el modelo no cumple con los supuestos del modelo.| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
| Un punto que está lejos de los otros puntos en la dirección x | Un punto influyente |
Utilice la gráfica de residuos vs. ajustes para comprobar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
Histograma de residuos
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Una larga cola en una dirección | Asimetría |
| Una barra que se encuentra muy alejada de las otras barras | Un valor atípico |
Puesto que la apariencia de un histograma depende del número de intervalos usados para agrupar los datos, no utilice un histograma para evaluar la normalidad de los residuos.
Un histograma es más efectivo cuando tiene aproximadamente 20 o más observaciones. Si la muestra es demasiado pequeña, entonces cada barra del histograma no contiene suficientes observaciones para revelar asimetría o valores atípicos de una manera fiable.
Gráfica de residuos vs. orden
Tendencia
Turno