Un ingeniero de un fabricante de equipos de golf desea diseñar una nueva pelota de golf que maximice la distancia de vuelo de la pelota. El ingeniero ha identificado cuatro factores de control (material del núcleo, diámetro del núcleo, número de dimples y grosor de la cubierta) y un factor de ruido (tipo de palo de golf). Cada factor de control tiene 2 niveles. El factor de ruido está compuesto por dos tipos de palos de golf: driver y un hierro 5. El ingeniero mide la distancia de vuelo de cada tipo de palo de golf y registra los datos en dos columnas de factor de ruido de la hoja de trabajo.
Debido a que la meta del experimento es maximizar la distancia de vuelo, el ingeniero utiliza la relación de señal a ruido (S/N) más grande es lo mejor. El ingeniero también desea probar la interacción entre el material del núcleo y el diámetro del núcleo.
- Abra los datos de muestra, BolaGolf.MWX.
- Elija .
- En Los datos de respuesta están en, ingrese Driver y Hierro.
- Haga clic en Análisis.
- En Ajustar modelo lineal para, marque Relaciones de señal a ruido y Medias. Haga clic en Aceptar.
- Haga clic en Términos.
- Mueva los términos A: Material, B: Diámetro, C: Dimples, D: Grosor y AB de Términos disponibles a Términos seleccionados. Haga clic en Aceptar.
- Haga clic en Opciones.
- En Relación de señal a ruido, seleccione Más grande es lo mejor. Haga clic en Aceptar.
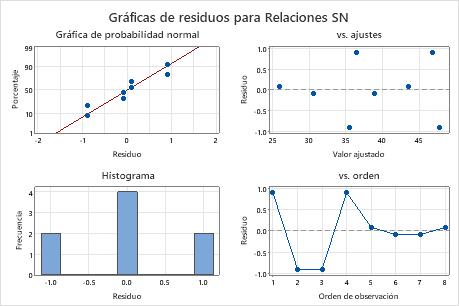
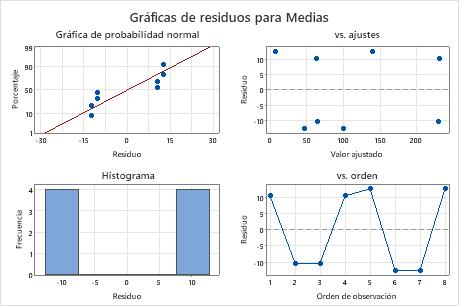
- Haga clic en Gráficas de análisis y, a continuación, seleccione Cuatro en uno.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
Minitab provee una tabla de coeficientes de regresión estimados para cada característica de respuesta que usted seleccione. En este ejemplo, el ingeniero elige dos características de respuesta: la relación de señal a ruido (S/N) y las medias. Utilice los valores p para determinar cuáles factores son estadísticamente significativos y use los coeficientes para determinar la importancia relativa de cada factor en el modelo.
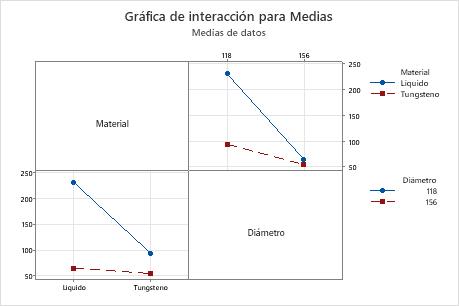
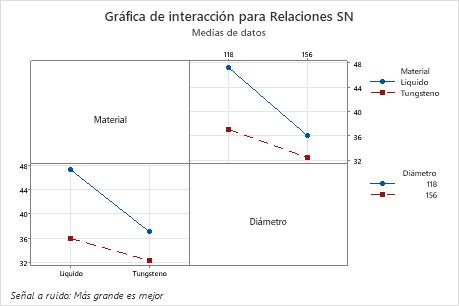
En este ejemplo, para las relaciones S/N, todos los factores tienen un valor p menor que 0,05 y son estadísticamente significativos en un nivel de significancia de 0,05. Frecuentemente, se utiliza un nivel de significancia de 0,10 para evaluar los términos en un modelo. La interacción es estadísticamente significativa en un nivel de significancia de 0,10. Para las medias, el material del núcleo (p = 0,045) y el diámetro del núcleo (p = 0,024) son estadísticamente significativos en un nivel de significancia de 0,05, y la interacción de material con diámetro (p = 0,06) es estadísticamente significativa en un nivel de significancia de 0,10. Sin embargo, debido a que ambos factores participan en la interacción, usted necesita comprender la interacción para poder considerar el efecto de cada factor de forma individual.
El valor absoluto del coeficiente indica la fuerza relativa de cada factor. El factor con el coeficiente más grande tiene la mayor influencia en una característica de respuesta dada. En los diseños de Taguchi, la magnitud del coeficiente del factor normalmente refleja el rango del factor en las tablas de respuesta.
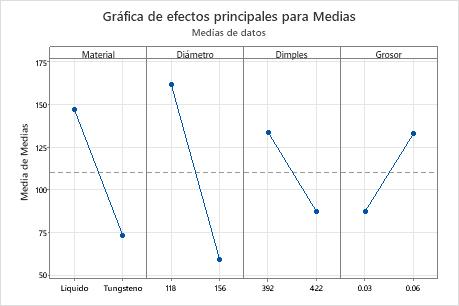
Las tablas de respuesta muestran el promedio de cada característica de respuesta para cada nivel de cada factor. Las tablas incluyen rangos basados en estadísticos Delta, los cuales comparan la magnitud relativa de los efectos. El estadístico Delta es el mayor menos el menor promedio para cada factor. Minitab asigna rangos basados en los valores de Delta; el rango 1 para el valor de Delta más alto, el rango 2 para el segundo más alto, y así sucesivamente. Utilice los promedios de nivel en las tablas de respuesta para determinar cuál nivel de cada factor provee el mejor resultado.
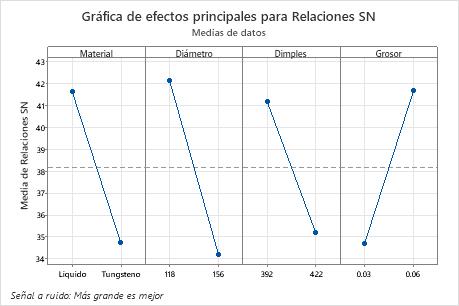
En los experimentos de Taguchi, usted siempre desea maximizar la relación S/N. En este ejemplo, las clasificaciones indican que el diámetro del núcleo (B) ejerce la mayor influencia tanto en la relación S/N como en la media. Para la relación S/N, el grosor de la cubierta (D) ejerce la siguiente influencia más grande, seguida por material del núcleo (A) y dimples (C). Para las medias, el material del núcleo (A) ejerce la siguiente influencia más grande, seguida por dimples (C) y grosor de la cubierta (D).
- Núcleo líquido (A)
- Diámetro del núcleo (B) = 118
- Dimples (C) = 392
- Grosor de la cubierta (D) = 0,06
Para continuar este análisis, el ingeniero puede utilizar Predecir resultados de Taguchi para determinar las relaciones S/N y metas pronosticadas en estos valores de configuración de factores. Para obtener más información, vaya a Ejemplo de Predecir resultados de Taguchi
Coeficientes de modelos estimados para Relaciones SN
| Término | Coef | EE del coef. | T | P |
|---|---|---|---|---|
| Constante | 38.181 | 0.4523 | 84.418 | 0.000 |
| Material Líquido | 3.436 | 0.4523 | 7.596 | 0.017 |
| Diámetro 118 | 3.967 | 0.4523 | 8.772 | 0.013 |
| Dimples 392 | 2.982 | 0.4523 | 6.593 | 0.022 |
| Grosor 0.03 | -3.479 | 0.4523 | -7.692 | 0.016 |
| Material*Diámetro Líquido 118 | 1.640 | 0.4523 | 3.625 | 0.068 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 1.2793 | 99.21% | 97.23% |
Análisis de Varianza de Relaciones SN
| Fuente | GL | SC Sec. | SC Ajust. | MC Ajust. | F | P |
|---|---|---|---|---|---|---|
| Material | 1 | 94.427 | 94.427 | 94.427 | 57.70 | 0.017 |
| Diámetro | 1 | 125.917 | 125.917 | 125.917 | 76.94 | 0.013 |
| Dimples | 1 | 71.133 | 71.133 | 71.133 | 43.47 | 0.022 |
| Grosor | 1 | 96.828 | 96.828 | 96.828 | 59.17 | 0.016 |
| Material*Diámetro | 1 | 21.504 | 21.504 | 21.504 | 13.14 | 0.068 |
| Error residual | 2 | 3.273 | 3.273 | 1.637 | ||
| Total | 7 | 413.083 |
Coeficientes de modelos estimados para Medias
| Término | Coef | EE del coef. | T | P |
|---|---|---|---|---|
| Constante | 110.40 | 8.098 | 13.634 | 0.005 |
| Material Líquido | 36.86 | 8.098 | 4.552 | 0.045 |
| Diámetro 118 | 51.30 | 8.098 | 6.335 | 0.024 |
| Dimples 392 | 23.25 | 8.098 | 2.871 | 0.103 |
| Grosor 0.03 | -22.84 | 8.098 | -2.820 | 0.106 |
| Material*Diámetro Líquido 118 | 31.61 | 8.098 | 3.904 | 0.060 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 22.9035 | 97.88% | 92.58% |
Análisis de Varianza de Medias
| Fuente | GL | SC Sec. | SC Ajust. | MC Ajust. | F | P |
|---|---|---|---|---|---|---|
| Material | 1 | 10871 | 10871 | 10870.8 | 20.72 | 0.045 |
| Diámetro | 1 | 21054 | 21054 | 21053.5 | 40.13 | 0.024 |
| Dimples | 1 | 4325 | 4325 | 4324.5 | 8.24 | 0.103 |
| Grosor | 1 | 4172 | 4172 | 4172.4 | 7.95 | 0.106 |
| Material*Diámetro | 1 | 7995 | 7995 | 7994.8 | 15.24 | 0.060 |
| Error residual | 2 | 1049 | 1049 | 524.6 | ||
| Total | 7 | 49465 |
Tabla de respuesta para relaciones de señal a ruido
| Nivel | Material | Diámetro | Dimples | Grosor |
|---|---|---|---|---|
| 1 | 41.62 | 42.15 | 41.16 | 34.70 |
| 2 | 34.75 | 34.21 | 35.20 | 41.66 |
| Delta | 6.87 | 7.93 | 5.96 | 6.96 |
| Clasificar | 3 | 1 | 4 | 2 |
Tabla de respuesta para medias
| Nivel | Material | Diámetro | Dimples | Grosor |
|---|---|---|---|---|
| 1 | 147.26 | 161.70 | 133.65 | 87.56 |
| 2 | 73.54 | 59.10 | 87.15 | 133.24 |
| Delta | 73.73 | 102.60 | 46.50 | 45.68 |
| Clasificar | 2 | 1 | 3 | 4 |