Matriz de diseño
En primer lugar, Minitab crea una matriz de diseño a partir de los factores y el modelo que usted especifica. Las columnas de esta matriz representan los términos incluidos en el modelo. Luego, Minitab agrega columnas adicionales para el término constante, los bloques y los términos de orden superior para completar la matriz de diseño para el modelo en el análisis.
Diseños con todos los factores continuos
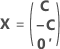
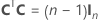
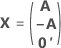
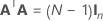
La matriz de diseño completa contiene columnas además de las columnas que representan los factores. La matriz de diseño contiene una columna de unos (1) para el término constante. La matriz de diseño completa también incluye columnas que representan los términos cuadráticos o de interacción incluidos en el modelo.
Diseños con factores categóricos
Para un diseño que incluye factores categóricos, Minitab sustituye la fila de punto central único de la matriz de diseño por 2 pseudo puntos centrales. Si el diseño solo incluye 1 factor categórico, solo existen dos pseudo puntos centrales posibles, así que ambos puntos están en el diseño.
En casos en los que el diseño tiene más de 2 factores categóricos, Minitab utiliza un algoritmo iterativo para seleccionar 2 pseudo puntos centrales para su inclusión. El algoritmo trata de minimizar la varianza de los coeficientes de regresión para los efectos lineales en el modelo.
Notación
| Término | Description |
|---|---|
| C | Una matriz de conferencia |
| 0' | Una fila de ceros en una matriz que representa una corrida de punto central |
| In | la matriz de identidad n × n |
| A | Una matriz que es un subconjunto de una matriz de conferencia con N filas y n columnas donde  |
| N | El número de filas en el subconjunto de las columnas de la matriz de conferencia |
| n | El número de factores en un diseño |
Coeficiente (Coef)
En términos de matriz, la fórmula que calcula el vector de coeficientes en el modelo es:

Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| Y | vector de respuestas |
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 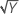 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Regresión ponderada
La regresión de mínimos cuadrados ponderados es un método para tratar las observaciones que tienen varianzas no constantes. Si las varianzas no son constantes, a las observaciones con:
- a las grandes varianzas se les debe ofrecer ponderaciones relativamente pequeñas
- a las pequeñas varianzas se les debe ofrecer ponderaciones relativamente grandes
La elección de ponderaciones generalmente es la inversa de la varianza de error puro en la respuesta.
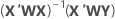
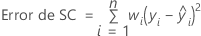
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
| W | una matriz n x n con las ponderaciones en la diagonal |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| wi | ponderación de la iésima observación |
| yi | valor de respuesta de la iésima observación |
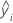 | valor ajustado de la iésima observación |
